Dear Reader,
Since the last time I posted, I have added the ability to generate a different lattice structure to the Sphere Packing software. This new lattice structure is called the hexagonal close packed (hcp) lattice. It is one of the tightest ways to pack equally sized spheres, with the other way being the face-centered cubic (fcc) lattice which only differs in the way that consecutive layers are aligned.
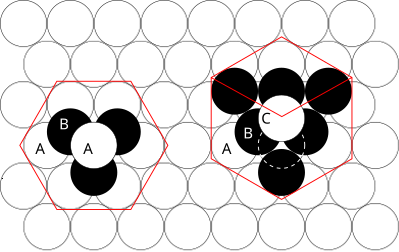
In the above image, a bird’s-eye view of hcp packing (left) and fcc packing (right) is shown. The underlying hexagonal arrangement of white spheres representing layer 1 resembles the tightest way of packing equally sized circles in a plane also known as a penny-packing. Every layer of the hcp and fcc lattices has this identical hexagonal arrangement. The black spheres representing layer 2 are placed over the gaps created between three underlying spheres. Note that layer 2 and layer 3 are not fully drawn out so that the lower layers are not obscured completely. Also note that layer 2 is identical for both hcp and fcc lattices. The difference is from layer 3 which lines up with layer 1 in the hcp lattice, but is shifted in the fcc lattice.
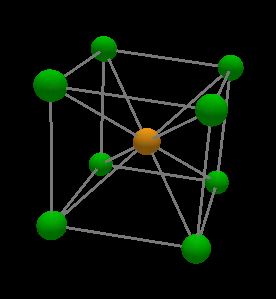
Anyways, back to the main point. Hexagonal close-packed lattices are now available to use in the sphere packing software. Earlier there was only body centered cubic lattices:


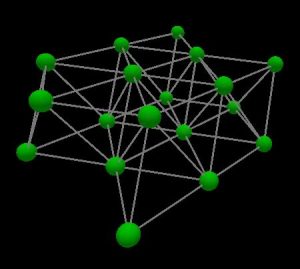
Now here are the hcp lattices:

With this new type of lattice we hope to gain insights into how a different set of combinatorics affects sphere packing.

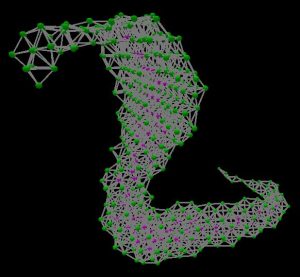
Moving forward, I would like to 3D print the meshes generated by the sphere packing. The difficulty lies in the fact that the meshes are not solids, so traditional 3D slicer programs can not work with the mesh output directly. Thus, one approach would be to convert the mesh into a solid. As it has been suggested to me, this could possibly be done using OpenSCAD. Another approach would be to skip the slicer step completely and directly generate gcode from the mesh using a toolpath planning algorithm. I will first try the method of converting the mesh into a solid since it seems easier than developing a new algorithm for toolpath planning in 3D space. I will keep you posted on the results.
Thanks for reading!
-Xiang
