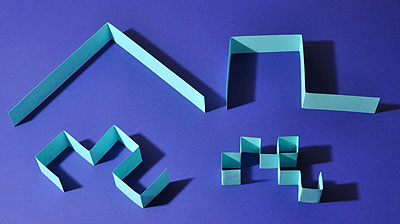Our first-day 3D print will be the Dragon Curve by UMF3D on Thingiverse, from the University of Maine at Farmington:
This is actually only the “seventh iteration” of the fractal known as the Dragon Curve; like many fractals, the true Dragon Curve is the result of applying a certain process infinitely many times, but the model we are printing is the result of applying that process only seven times.
Start your prints!
We have three different types of 3D printers in JMU 3SPACE, and each one operates a little differently. The Afinias are operated from the computer with the “3D” software. This software opens STL files, slices them, and sends them directly to the printer. The Ultimaker printers are operated from their own screen an jog wheel, with files on an SD or USB card that were previously sliced the the software “Cura”. We’ll learn more about this later on; right now we just want to print something!
To start a Dragon Curve print on an Afinia:
- The “3D” software should already be open on your computer, with model already be loaded and proper settings already in place.
- From the “3D” software, choose the 3D Print drop-down menu from the very top of the screen (*not* the button icon labeled 3D print), and select Table Heat 15 mins.
- Now press the 3D Print button, which inexplicably looks like a 2D paper printer, then press “OK”.
To start a Dragon Curve print on an Ultimaker:
- The model should already be sliced and ready on an SD card or USB drive inserted into the front of the printer.
- Move the jog wheel on the front of the machine to select Print, and press the jog wheel like a button.
- Use the jog wheel to select the file UM2E_dragon7 or UM3_dragon7, depending on the model of your machine, and press the button when that file is highlighted.
What is the Dragon Curve?
Below is an Wikipedia animation of a sequence of iterations of the Dragon curve, starting from a simple right angle and getting more complex each time. Note that as the interations increase, the one-dimensional curve starts to fill what seems to be a two-dimensional shape. Also, in the later iterations you can see the Dragon Curve seems to have smaller copies of itself inside of itself (!).

There are many different ways that the Dragon Curve can be generated. Here are three of them:
Method 1: Replace lines with right angle shapes, then repeat
As described in the Wikipedia article: “Starting from a base segment, replace each segment by 2 segments with a right angle and with a rotation of 45° alternatively to the right and to the left.” This is perhaps the hardest of the three methods to visualize, but when we learn about recursive coding methods and fractal dimension later on, this method might turn out to be the easiest.

Method 2: Unfold by rotating a new copy of each iteration by 90 degrees
Put two idential iterations on top of one another and pretend they are hinged at one end, then rotate the top copy 90 degrees. You can try this with multiple copies of the Seventh Iteration Dragon Curve that we are 3D printing in class. Two copies of the Seventh Iteration will make the Eighth Iteration, then two copies of the Eighth Iteration (which is four copies of the Seventh) will make the Ninth, and so on.

Method 3: Fold paper in half over and over
Take a long strip of paper and fold it in half, then in half again the “same way”, then in half again, and so on. Unfold the paper to make a sequence of right angles; this will be an iteration of the Dragon Curve! In some sense this is just the reverse of the method above, if you think about it. Here is an image of the First through Fourth Iterations with paper-folding, from CutOutFoldUp:
And finally, here is a great Numberphile video about the paper-folding method of constructing the Dragon Curve:
Future questions
- What generalizations or modifications of the Dragon Curve might be interesting?
- The Dragon Curve is a space-filling curve; what does that mean?
- Multiple Dragon Curves will tile the plane; what does that mean?
- Is there a three-dimensional analogue to the Dragon Curve?
- What sorts of 3D models of the Dragon Curve have people already created, and how could we take that work a step further?
- What could we 3D print to enable us to easily make a large-scale model of a high iteration of the Dragon Curve?