The first fractal I want to print is the Koch Snowflake. According to fractal.org, in an article by Edyta Patrzelk, in order to create a Koch Snowflake, you must begin with an equilateral triangle. It claims the length of the boundary is 3 x 4/3 x 4/3 x 4/3…-infinity, but I have no idea what that means, yet. I love this because although it starts out as a simple triangle, it quickly turns into a snowflake; who doesn’t love snowflakes?
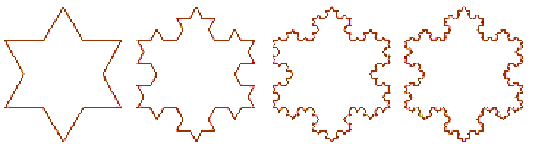
On the Wikipedia page for the Koch Snowflake, it shows a GIF if what it looks like to zoom into the edges of the Koch Snowflake. After watching it several times, I realized it isn’t just a loop, it the constant additions of sides as the fractal is constructed.

After watching a few videos about the Koch Snowflake, I found this video by the Washington Student Math Association.
Similar to what Dr. Taalman showed the class today, the student in the video began with a simple structure (a triangle) on a white board and erased the lines as she continued, eventually creating a Koch Snowflake. As I was watching this video, I began to understand how a simple triangle can turn into the Koch Snowflake itself. Also, it made more sense of the numbers that were given in the description on how to continually construct the Koch Snowflake.
While searching on Thingiverse, I found a Koch Snowflake that seemed perfect to remake. Although it looks a little more complicated than the one shown above, I think it is even better looking. Also, that confirms for me that it is printable because others have remade it and printed it themselves. I believe this fractal could print at about 60 millimeters.
3D Printing Results

I believe my Koch Snowflake came out perfect! I printed it on the Afinia and it came out the perfect size. Although it was the simplest one on thingiverse, I still believe that it looks really cool.