Group Members:
Jenna Jordan (Writer)
Isabelle Murakami (Designer)
Megan Shanian (Math Consultant)
Project Idea:

Our project idea is to create a print of elliptical Borromean rings from chapter 8 of our book. Borromean rings often contain three rings, but can contain up to four or five. We are going to start out with a three ring print because it is the most simple way to make Borromean rings, then we are going to try to design one with four rings. One unique property about Borromean rings is that if you cut one of the three rings, the other two rings separate as well. When we print the rings, we can print one and then place it inside of the next ring we are printing as a simple way to get them to all fit together. Another way we could print the rings is by printing them all separately with a small slit in them and then put them together and glue them. While we haven’t figured out exactly how we want to print the Borromean rings, we know that it is definitely doable and it was really exciting to see Professor Taalman’s 3D print of the rings in the book!
First Steps:

When it came to creating our design on Tinkercad, the majority of class on Thursday was spent trying to get the perfect shape rings to make the design work. Our major challenge is that the rings need to be the exact same size, with one ring fitting inside the other at a 90 degree angle. This means that Isabelle had to very carefully tweak the rings to be the perfect thickness and oval shape to fit without touching each other. By the end of the class period we were able to design two rings that do not touch each other, and we started to plan out how to include a third ring.

Design Process:
After adjusting the ring sizes and angles to a configuration that could print and fit together, we printed each component separately and fit them together. To do this, we had to design one ring with a small slit in it so that we could fit it through the other two rings. This slit also allows us to show the unique property that when you remove one ring, the other two come apart. After several days of trying to print two rings with support and fit one in, we realized that it is easiest to just print all the rings separately, no matter what level you’re printing.
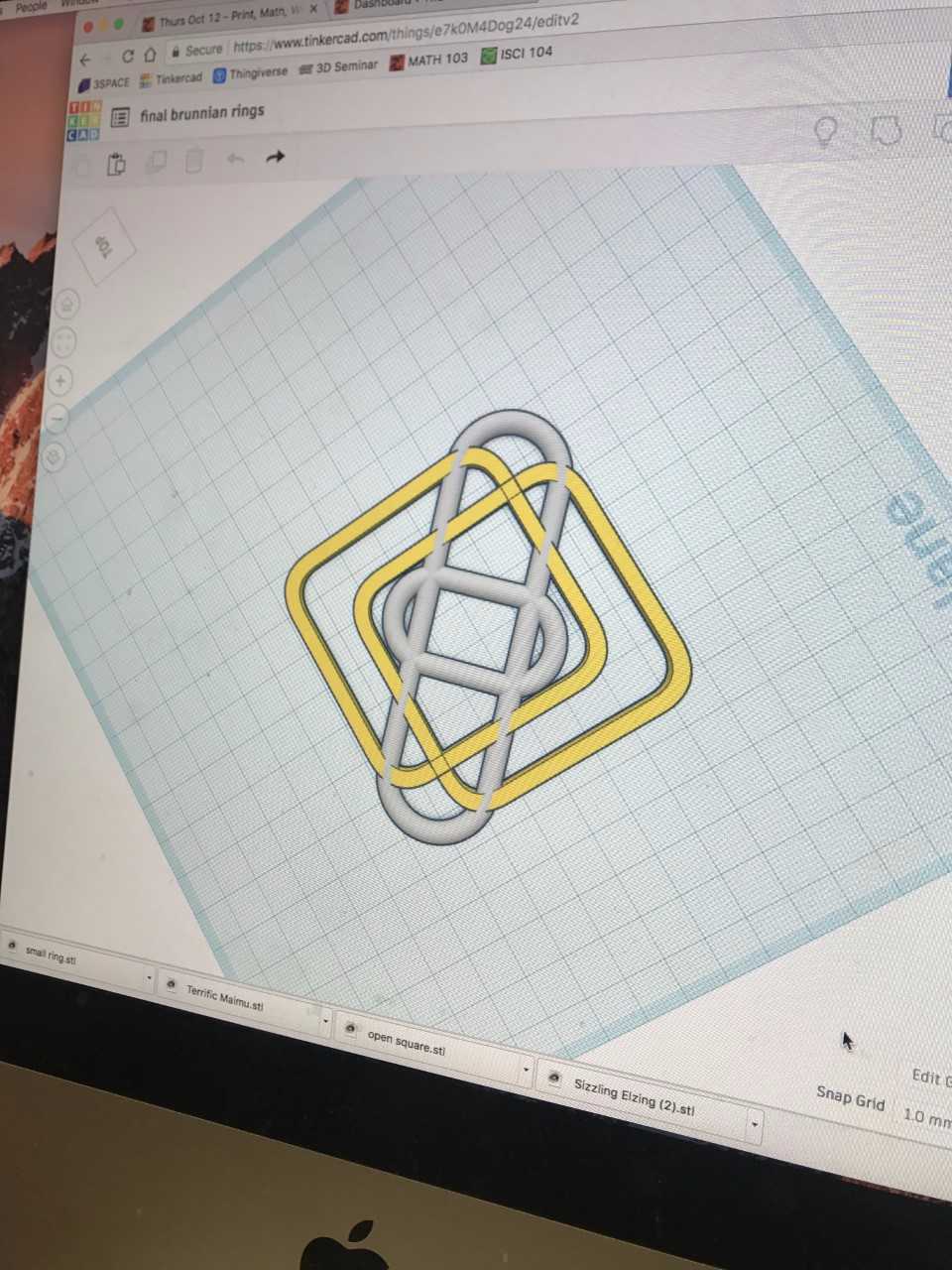
After we successfully printed the level 3 Borromean Rings, we were tasked to attempt to design and print a level 4. When it came to the level 4 design, we had to figure out how to make the print work in 3D when we only had a 2D picture to reference. With this design, we didn’t have to worry about making all the rings the exact same size. We did have to make sure that the rings had enough space to fit 4 rings together. Below is a photo of how we used Tinkercad to make sure that we could design the level 4 Brunnian link that could actually fit together in 3D.
Final Print of Borromean Rings:
Luckily, we were able to print the rings in three different colors to show how they all intersect with each other. We were able to get the perfect size slit in one ring so that the three rings can stay connected and shoe the 3D properties of our design. After successfully printing the Borromean rings, we were able to print the level 4 Brunnian link. We printed it at the end of Tuesday’s class so we did not have a chance to insert a picture into this post.

The Mathematics of Borromean Rings:
Borromean rings are not solely a math concept, they appear in the world in various ways. One of the examples we found was in the advertisements/logo for a beer company. The company uses the three rings to symbolize the trinity of purity, body, and flavor. It is not uncommon for symbols like this to appear as a message of a trinity or balance of three things. However, looking at this advertisement critically should raise questions. Is it possible to have three perfect circles intersect in a functional way?

A key aspect of Borromean rings is that they are dependent on each other. If you remove one ring, the other two rings will separate. The most common image that comes up when you research Borromean rings shows three perfect circles interlocked. This is misleading and inaccurate because it is not possible to create the rings with perfect circles in real life.

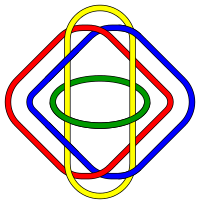
The configuration has many different levels as well. Going all the way up to 4, 5, or even 6 levels, the rings depend on each other. Borromean rings only function if they are in the shape of an ellipse (a flattened circle or oval), because of the way they weave through and connect to each other. Borromean rings cannot be circular because when the first two rings are placed, they would form the shape of a sphere, meaning the third ring would have to touch the other rings in 4 places, which is impossible. When moving to levels 4 and above, the Borromean rings become what is known as a “Brunnian Link”. After doing some external research, we learned that when you cut the rings, one iteration is equivalent to a braid and tying the ends of a braid will result in a Borromean ring. Below is a photo of a level 4 Brunnian Link. As you can see, when you move up from a level 3 Borromean Ring, the rings so not all have to be ellipses. There is a helpful article that explains that although Borromean rings are often depicted as perfect circles, they can only be successfully created using ellipses or bent circles. Here is the link to our Thingiverse page where we uploaded our final designs, as well as our Tinkercad page.