Group Member Roles:
Designer : Collin Cullen
Math Consultant : Yang Zhou
Writer : Sam Janssen
Project Idea:

For our open project idea, we decided to experiment with the relationships of the “perfect pizza slice” with its self and with the pizza as a whole as a solution to the pizza problem. The goal of the pizza problem is to find how to cut a pizza into same shaped slices that don’t all touch the middle. We want to print this as one slice of the pizza 12 times to show that it is one shape repeated to perfectly fill the area of the pizza. One must assume the pizza is flat, as to not cut it horizontally, before attempting to solve or demonstrate the solution for the pizza problem.
First Steps:

We created a vector of the exact shape we will need to test the “perfect pizza slice”. Vectoring the shape in a 2D space was much easier than modeling the shape in a 3D space. We put the vector into tinkercad and extruded it into the proper object we needed and began to print just a few copies to make sure it would fit right. The class ended before our print did so we have yet to figure out what adjustments to make if we need to make any. It turned out that we needed to adjust the curves in order for the sides to fit together in a full circle. We had to do a lot of back and forth between printing, vectoring, and modeling.
Design Process:

Our design is fairly simple, as it was provided to us by the book. The design in the book was 12 shark fin triangle shapes in a circle. The challenge came when reproducing the individual pieces of the perfect pizza in 3D space. Our first step was to create a digital line drawing that we could import into tinker cad and extrude into 3D shapes. Making the piece was a bit difficult because they all need to fit together and be fairly precise. After a lot of back and forth between the line drawings, tinker cad, and printing on the Ultimaker, trial and error resulted in a pretty refined slice of pizza. We decided to print 4 at a time 3 times for a total of the 12 piece needed to compose a whole pizza.
We had to print a set of 4 pieces several times before we got the curves right. The first version with one flat edge was fitting together, but not second version with all curved sides. We had to go back to the original drawing and fix the curved edges to try and model then print. It took a bout 3 or 4 tries until we got the curves close enough for all 12 pieces to fit together.
Final Prints:



After a bit of back and forth between the design and the printer we finally managed to fit all our pieces together. We decided to print all 3 slutions, the two from the book, and the one that we came up with on our own.
The Math of The Perfect Pizza:
The math for our pizza is fairly simple. In order to find a solution to the pizza problem and create equal sized pizza slices that don’t all touch the middle, we used the same arc of the original pizza’s circumference to divide the pizza into 6 parts. Once more, to create 12 equal parts, we divided each of the 6 parts in half. Now we have 12 equal parts, 6 pieces along with their mirrored counterparts, of a pizza that don’t all touch the middle. Another way to divide each of the base 6 parts in half is by using the circumference again creating more of a claw shape. This eliminates the need to have mirrored shapes and every single piece is truly same shape.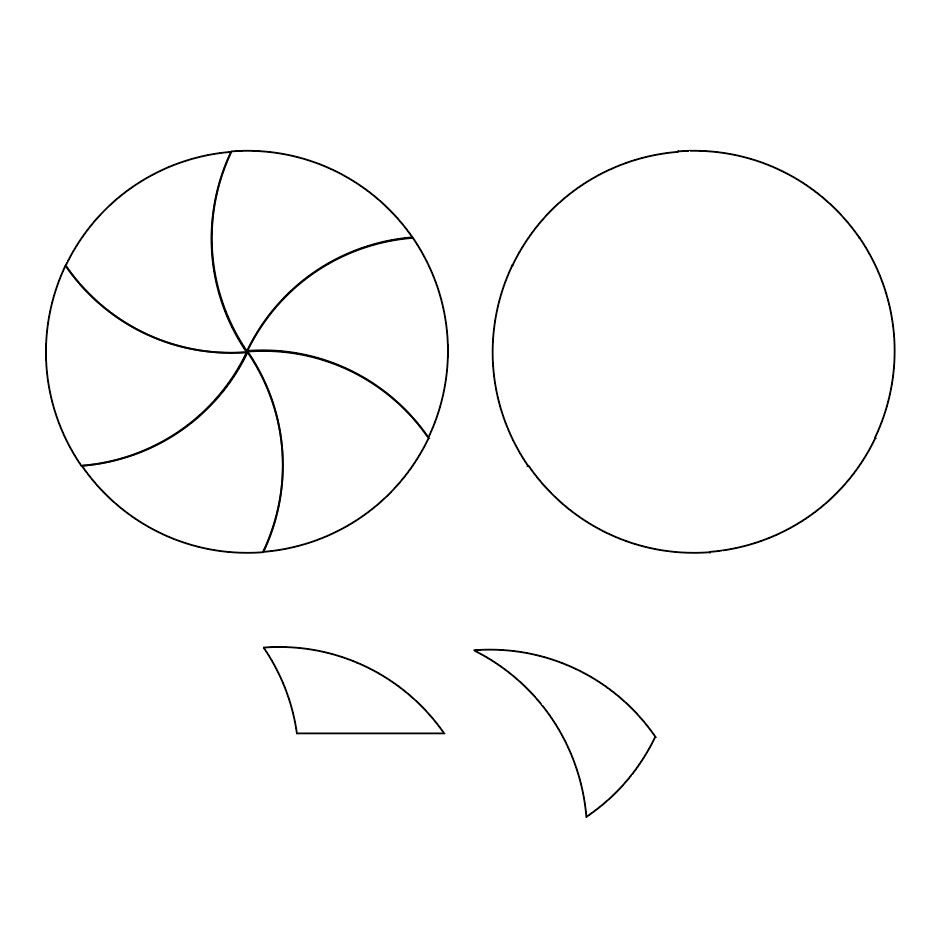
A: πr 2
(πr 2)/12 = Perfect Pizza Slice
This takes the total surface area and divides it into the 12 equal pieces.
After creating the solution of the Pizza Problem provided to us from the book, we tried to find our own solution. We immediately decided that 12 pieces was much to many, logistically, so we decided to divide the pizza into 5 pieces. The main idea of the previous solutions was using the same arc of the circumference for each cut, so we chose to use the entire circumference to divide the pizza into the 5 slices, creating rings. To do this we worked backwards from the outer ring’s circumference.
Total Area: 12265.625, r= 62.5
√12265.625/π= 62.5
Inner Circle 1: 9812.5, r= 55.9
√9812.5/π= 55.9
Inner Circle 2: 7359.37, r= 48.4
√7357.37/π= 48.4
Inner Circle 3: 4906.25, r= 39.5
√4906.25/π= 39.5
Inner Circle 4: 2453.125,r= 27.8
√2453.125/π= 27.8
Here are the rings and their outer radii visualized:
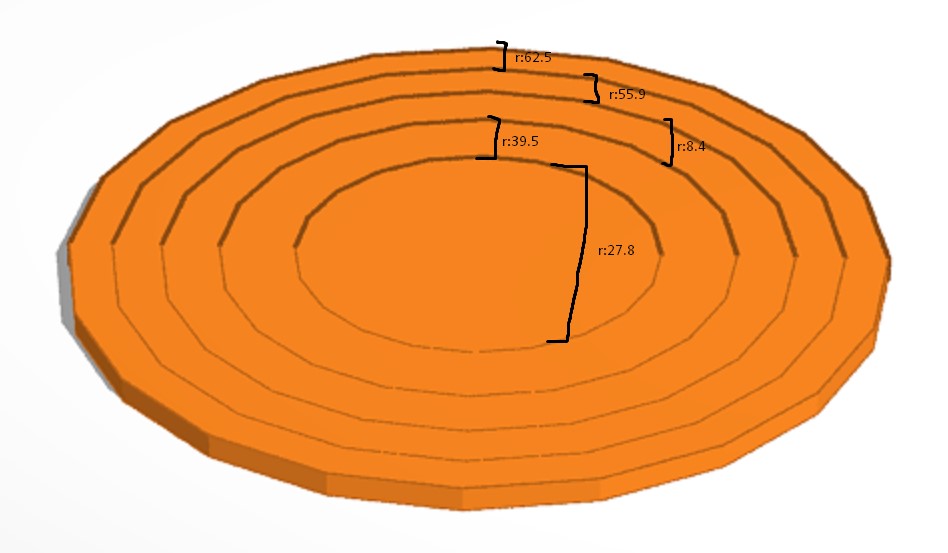
Now that we have the area of each circle that is .2, .4, .6, and .8 of the original circle, we subtract each area from the adjacent larger circle to make 5 rings of equal area. Each ring was 1/5 or .2 of the original circle. This is a solution to the pizza problem, as we have all equal slices that don’t all touch the middle.
Ring 1: 12265.625-9812.5= 2,453.125
Ring 2: 9812.5-7359.37= 2453.125
Ring 3: 7359.37-4906.25= 2453.125
Ring 4: 4906.25-2453.125= 2453.125
Ring 5: 2453.125