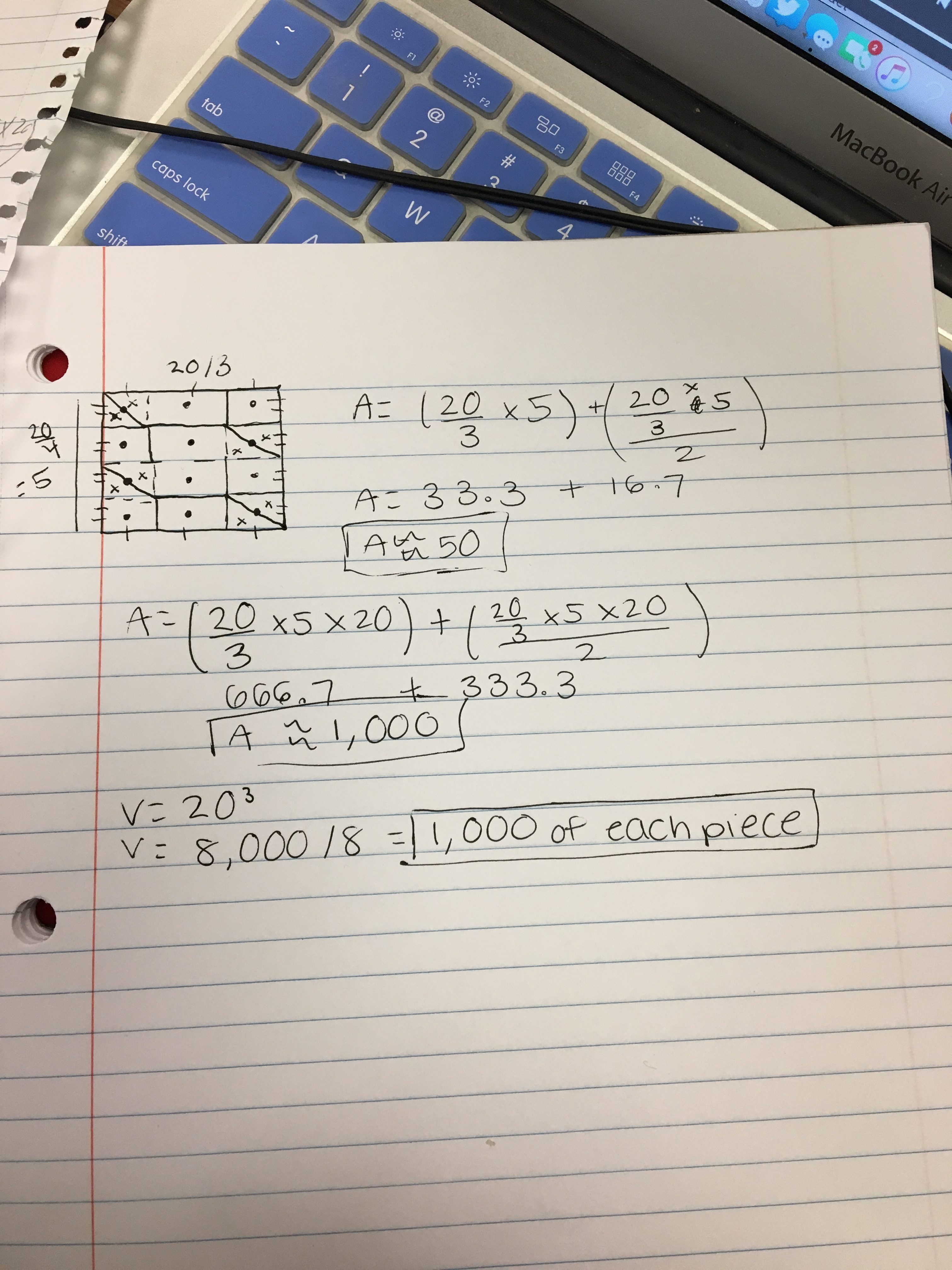Group Member Roles:
Dillon Call: Writer
Jiahao Guo: Designer
Katy Wagner: Math Consultant
Project Idea:
My group members and I originally wanted to look into Chapter 4 of Things to Make and Do in the Fourth Dimension by: Matt Parker. However, we decided to switch and do our project on cutting a cube to be equal in volume no matter how many slices it is cut into. If 5 people wanted to share a cube shaped cake with equal amounts of cake and icing for everyone, the cake would need to be cut into pyramids. The size of the triangles will be different, but the volume is the same due to the property of triangles that states as long as the base number is the same, the volume will be the same. Our project is going to cut slicing a cube into equal parts as shown in the book on page 42.
.
First Steps:
Our imaginary cake is going to be a cube. We tried to recreate the picture on page 42 under the heading A Non-Traditional Way to Cut a Cube-Cake. The cake is cut into 5 pyramids of different shapes while still having equal volume. We decided to cut ours into either 4 or 6 pieces instead. The problem is that we have no mathematical formula to ensure that our pieces are actually the same size. We began researching the problem and have found several different ways to cut our cube, so we’re going to try and find an easy solution without going down the traditional route.
Design Process:
It took us a few classes to come to this design. At first, we weren’t exactly thinking outside of the box. We tried to do an hour glass figure, but we couldn’t figure out how to make all of the pieces equal in volume and preference. In addition, we tried to use a circular shape for the cake, and we again couldn’t make everything equal. Finally, we settled on the design we ended up using to print.
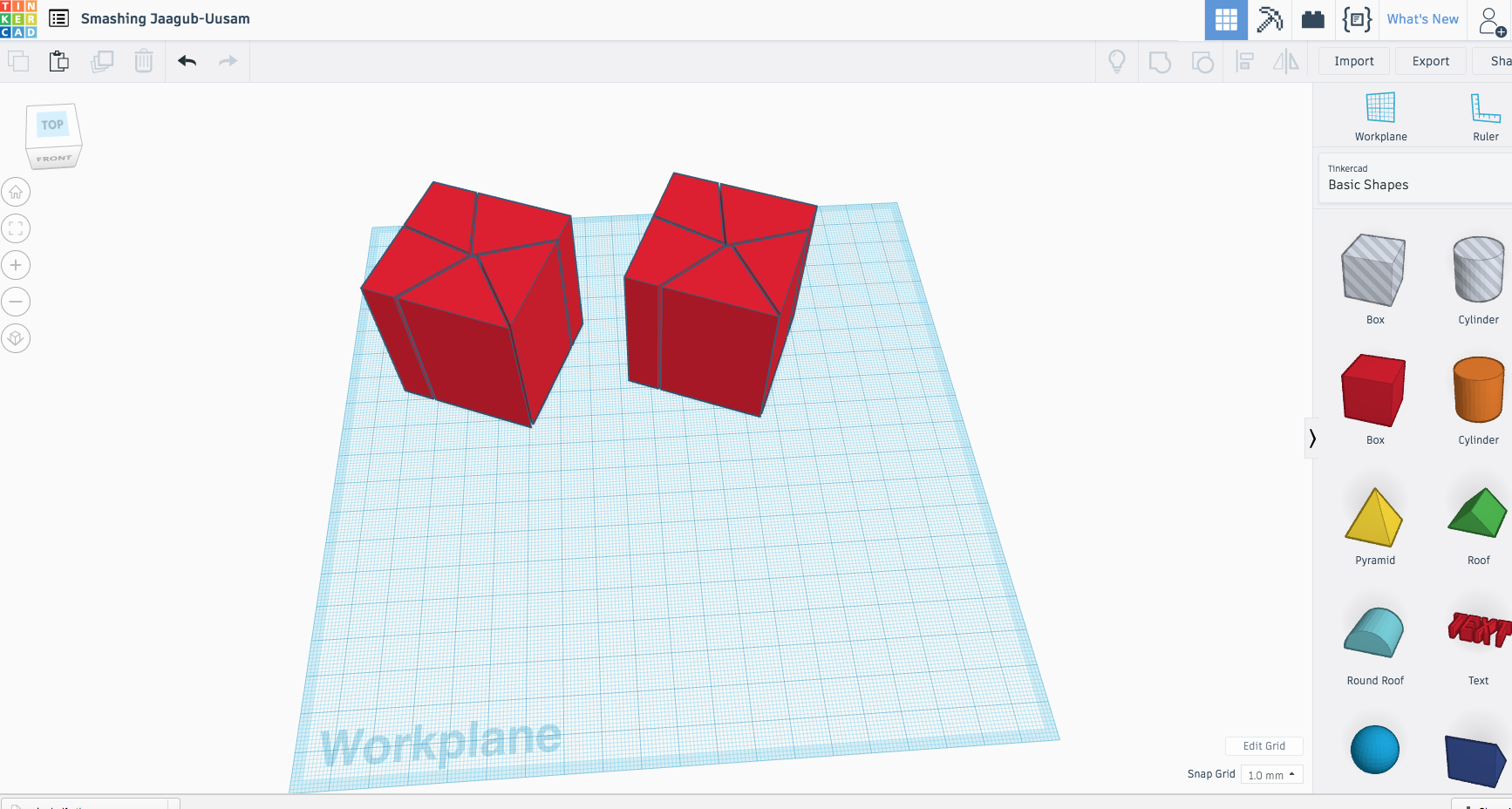
Final Print
We made our first print on the Afinia because we wanted to be able to take our print off of the supports. Here is what it looked like before we separated it:

Our second print is just a smaller version with a base on it made from the Ultimaker 2. We are also going to print a box to hold our pieces of the cake. We wanted our print to be interactive when explained, so we can demonstrate the cutting process by taking pieces away. We created our print on tinkercad, and we added it to thingiverse so other people could see it and make it too. Here are our finished products!

The Problem Explained:
Everyone loves cake, but some people have different preferences when it comes down to eating it. The issue is how to cut a cake for n number of people so everyone gets their preference while having the same volume. For this explanation, let’s assume the cake is a cube. You could cut it normally like this:
That would mean everyone got the same amount of cake, but it doesn’t necessarily mean that everyone got their preference. Even though the volume is equal, the perceived value of each piece is unequal meaning that not everyone is happy with their share. This is what we were talking about earlier with everyones preference of toppings, flavor, etc. We decided to study this project because all of us enjoy eating cake and mathematical cake cutting was a very interesting concept that we’ve never heard of before. Mathematicians find this process interesting because they would like to find an envy-free way of cutting a cake among any number of people. Many researchers believed that fair division was most likely impossible. They were convinced that there was no envy free algorithm for dividing cake among many people. Our models show how we cut the cake equally amongst others. Within the past year, two computer scientists discovered an envy free algorithm for cake cutting that depends on the players. It is very complex but they are still continuing to change the algorithm to make it more simple.
The solution of our design is called equitable division. The equation that needs to be followed is Va(Xa) = Vb(Xb).
X= the piece of cake that one gets
V= the value that everyone gives their piece of cake
This process had to make every piece of the cake equal in area and volume. The cake was then sliced into different shapes but were equal in volume and area, making every piece of cake equal even though they may be different shapes. When equitable division comes into play, everyone will get a piece of cake that will be the same size, but it may not have the amount of frosting or cake that they desire. All of the pieces are the same size in this fractal. We first separated the cube into 12 smaller cubes. We labeled each small cube Q1, Q2, Q3 and so on. Q1 is located on the upper left hand corner of the cube and is split in half. Q6, Q7 and Q12 are also split in half in this cube. The small cubes split in half (Q1, Q6, Q7,Q12) then make 2 right triangles within the cube. The bigger cube is further cut by splitting it in half from the middle line. Between Q2, Q3 and Q5 these pieces are split evenly as well as Q4. The top half of the cube is then divided into two sections. The first section is made up of the top right triangle of Q1, Q2, Q3 and the top right triangle of Q6. The second section is made up of the bottom right triangle of Q1, Q4, Q5 and the bottom right triangle of Q6. The bottom half of the cube is also divided the same way the top half is divided. These sections end up being equal because there are four small cubes in each section, two whole small cubes and the two right triangles that make up a whole small cube, making each section equal to each other. The diagram in the photo below further explains how the cube is divided.