Group Member Roles:
Designer: Grant Folsom
Math Consultant: Summer Xia
Writer: Taylor Zabinsky
Project Idea:

Our project idea is to make a Prince Rupert’s Cube. The Prince Rupert problem was proposed by Prince Rupert of the Rhine, Prince Rupert’s cube is the largest cube that can pass through a hole cut through another cube without splitting the cube into two pieces. This proposition was developed through a bet that Prince Rupert made and took around 100 years to solve. This spare capacity is normally used to reinforce the edges of the hexagon hole and a cube. According to Wikipedia, the construction of a physical model of Prince Rupert’s cube is made challenging by the accuracy with which such a model needs to be measured, and the thinness of the connections between the remaining parts of the unit cube after the hole is cut through it.
First Steps:
Initially, we worked on our design, figuring out the logistics of how we are going to print it. We had to solve the problem of how one cube fits inside another cube. After working on multiple designs, we finally learned that one square has to be tilted at a 45-degree angle in order to fit into the other. We then created a hole on one cube from the shape of the other cube. Lastly, we added small curves connecting one plane to the other to ensure that it has support for printing.

Design Process:
The initial design was to have the second cube tilted at a 22.5-degree angle. It was then changed to 45 degrees in order to allow the second cube to pass through the first. When the platform was first created, the main concern was keeping the platform stable. Rings were added to keep the platform (cube one) together. When the first iteration underwent a print, it fell apart during the printing process. The rings were redone, made flat instead of round, for better stability and printing process. The second print also had supports which ensured a solid structure and allowed the print to come out better. The second iteration ended up working seamlessly; the cube could fit inside of the platform very nicely.

Final Print of Prince Rupert’s Cube:

The Mathematics of Prince Rupert’s Cube:
Before we start, think about any objects or shapes fitting inside of one another. The first thing that might come to mind is a child’s toy, where one has to try to fit each shape in the corresponding hole. What if it was possible to fit one single object through 3 different ones? Well, this is actually possible. A round-square-triangle is a single object that is able to fit through a 2D square, circle, and triangle. The original design was based off an internet image where the holes were constructed on different planes like a cube figure. Unfortunately, the print failed to maintain the shape for the piece to fit through. The “hole” was remade to a flat design, becoming the final print. The piece itself, designed to fit through the three holes, is designed with the three-dimensional shapes. (Cube, cylinder, and a pyramid).

So what is the problem? What is the largest cube that can pass through a cube of a given size?
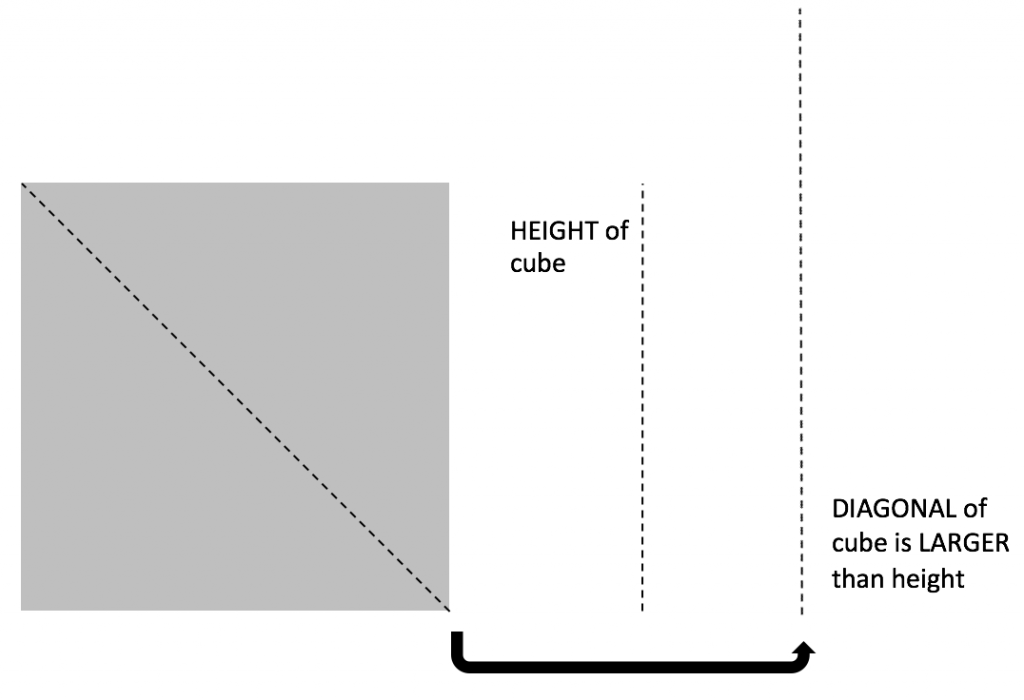
Let’s start simple, by fitting two equivalent sized squares inside of each other. As shown in the diagram below, one can see that the height of the square is distinctly shorter than the length of the diagonal. Using the Pythagorean theorem, one can figure out that the length of the diagonal for this square is actually √2. This means that two squares of equal size can pass through one another on a diagonal, with extra room to spare, as displayed in the diagram below.
*all of the remaining images below were created by Taylor Zabinsky in Word*

Now let’s move on to the cubes. Again, by using the Pythagorean theorem we know that the length of the diagonal for the cube is √3, which is even larger than the diagonal of the square. This means that two cubes of equal size can definitely pass through one another on a diagonal, with extra room to spare, meaning that an even larger cube would be able to pass through.
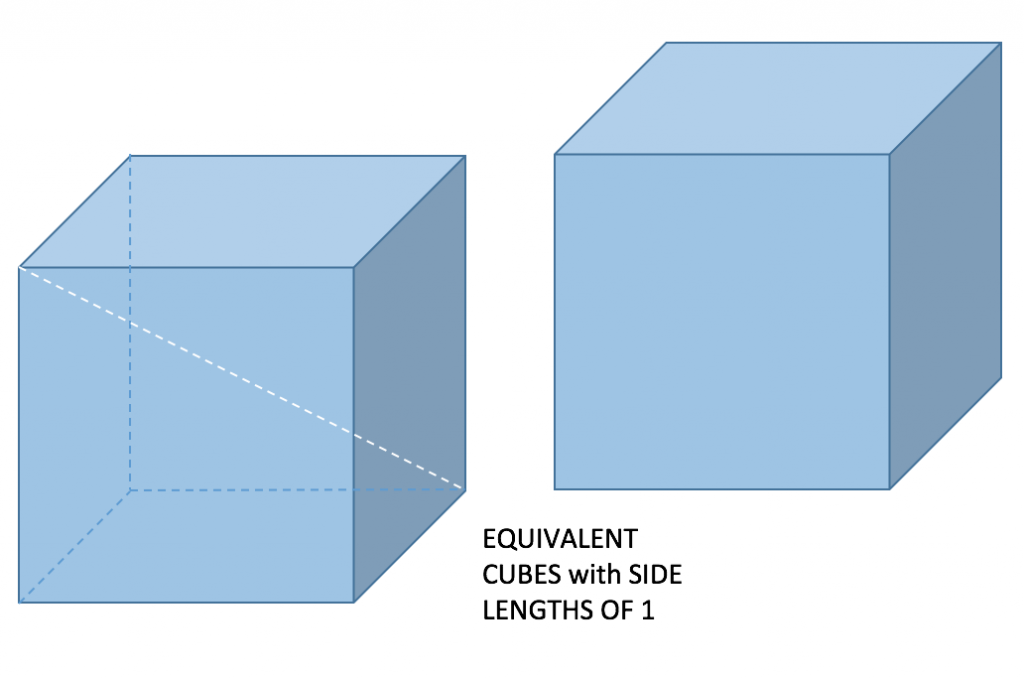
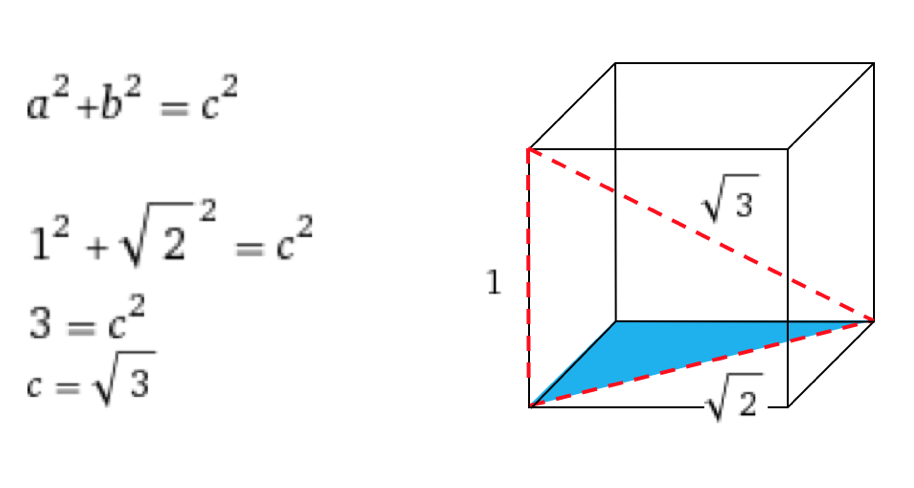
Is it possible for a larger cube to fit inside the first cube? If so, how much larger? Well if the original cube has a side length of 1, you know that the other cube can be slightly larger than one, a cube that passes through by barely touching the edges of the diagonal. In other words, a cube that has a side length of the diagonal of the original cube would be the largest cube that can pass through. Below I created a diagram showing the math of how it works. Again, using the Pythagorean theorem, you can solve for C or the length of the largest cube that can pass through.

To visually prove this proposition, take a cube and look along the body diagonal (corner to corner), you see the profile of a hexagon. You can put a square in this hexagon whose side length is greater than the original side length of the cube. This means that you can pass a larger cube completely through a smaller one.
Therefore; the solution to the problem is a maximally sized inner cube with sides of length 6% or 1.0606″ (3 sqrt(2))/4) larger than the unit cube with side lengths of 1.


Thingiverse & Tinkercad
You can find our design for Prince Rupert’s cube on Thingiverse here and Tinkercad here.
You can find the design for the square-circle-square on Tinkercad here and here.