The Plaid Carpet design was made by removing four blocks from level 1 coordinates [0,0], [3,0], [0,3], and [3,3].

Level 1
The surface area for level 1 would be the number of boxes removed, 4, times the area of the big boxes, (1), from the number of boxes that comprise the total area of the complete square, (16).
Therefore the equation would look like 16 – [(4)(1)] = 12. So level 1 has a surface area of 12 units.

Level 2

For level 2 we are going to find the area by finding the sum of the total number of removed boxes (4) x the surface area of the medium boxes (1/16) x the number of times 4 boxes were removed (12). This sum would be subtracted by the level 1 portion of the formula, so the equation would be 16 – [(4)(1)] – [(4)(1/16)(12)]. We want to put this equation into geometric series format, so we will simplify (1/16)(12) into 12/16 by using the laws of basic algebra. 12/16 is the r value of the geometric series variables ar, while the a value is 4.
Now the calculations will look like 16 – [(4)(1)] – [(4)(12/16)]=9.
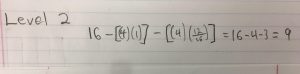
Level 3
For level 3 we are going to find the surface area by subtracting the total of the number of removed boxes (4) x the surface area of the small boxes (12/16)^2. Since this is another iteration of the fractal we are raising the r value to the number of iterations of this level. We subtract that sum from our previous area for level 2.
So the equation would be 16- [(4)(1)] – [(4)(1/16)] – [(4)(12/16]=6.75.
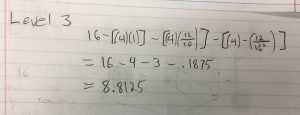
With the third level of the fractal I have now removed 4 boxes, 12 times, 12 more times. Which is why (12/16) is squared in the equation—> (12/16)^2.
Infinite Geometric Series Calculations
Dimension Calculations
To find the dimension of the Plaid Carpet Fractal I will use the formula (scale-down factor)^(dimension) = 1/(number of copies). The factor for how much the fractal will scale-down with each level is 1/4th. The number of copies is 12 because as was illustrated in the pictures and represented in the surface area calculations, the pattern is replicated 12 times more in each iteration.