Background:
In order to make my fractal, I removed the points: (1,1), (2,0) and (2,1). Removing these coordinates resulted in my fractal having an “L” shape pattern. In the second iteration of this fractal, the “L” shape attaches to the top of an upside down L, forming what look like dog ears. Below are levels 1, 2 and 3 of my fractal carpet.


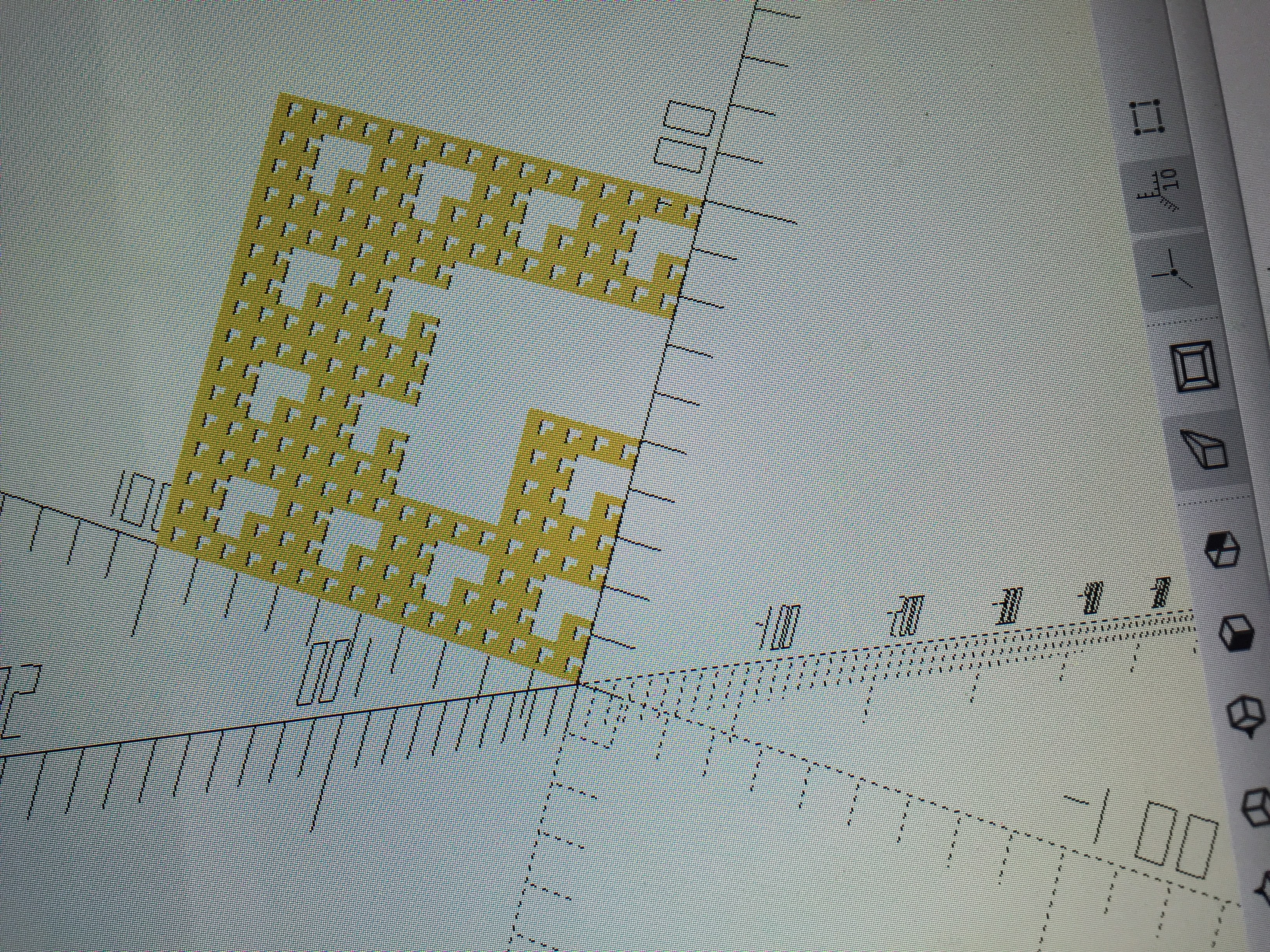

Math:
It took me a while to figure out the correct math for this fractal but eventually, everything ended up working out. What helped me determine the correct numbers for the higher level iterations was a developing pattern within the numbers. With each new level, the 3 stayed constant because no matter the circumstance, 3 boxes were taken out. To account for the size of the boxes, I realized that the fraction (13/16) stayed constant; the only differentiating component was the power of the fraction. With each level, the power of the fraction was increased by 1.
After figuring out the pattern, I was able to discover the “a” and “r” values.
a=3
r=13/16
Having these values set, the math became easy. After plugging these numbers into the formula for the sum of an infinite series:
A x (1/1-r), my answer came out to be 16.
For my final step, I plugged 16 into the equation; A= 16- (sum of infinite series)
A= 16-(16)
A=0
Explanation:
- Because A= 16- (sum of geometric series)… and the sum of my geometric series calculation came out to be 16 )…….(16-16=0)A=0

Area:

Levels 1 2 and 3 Area Calculation Explained:

Dimension:
In every fractal created by the class for this assignment, each square was scaled down by (1/4) in order to achieve the repeating pattern. The little square is 1/15 of the whole fractal. Within one of the large boxes, there is a smaller copy of the whole fractal. For my fractal, the larger copy is 13 copies of the smaller one.
Mathematically, we use logs to figure out this fractal’s dimensions. As seen on the calculations sheet, the formula to calculate dimension is logA(B)=D
When I plug in my fractal’s information into this formula, the numbers read: log 4 (13) = D.
I went to wolfram alpha in order to calculate the dimension, and it came out to be 1.85.

Thingiverse Link: