The Film Fractal Carpet is made by removing four blocks, two opposing each other in pairs. The coordinates removed are (0,2), (0,3), (4,2), & (4,3). The sequence of pictures shows the sequence from level 1-3.



Fractal Calculations
Before any calculations are done, look at this sample to know where some of the calculations come from.
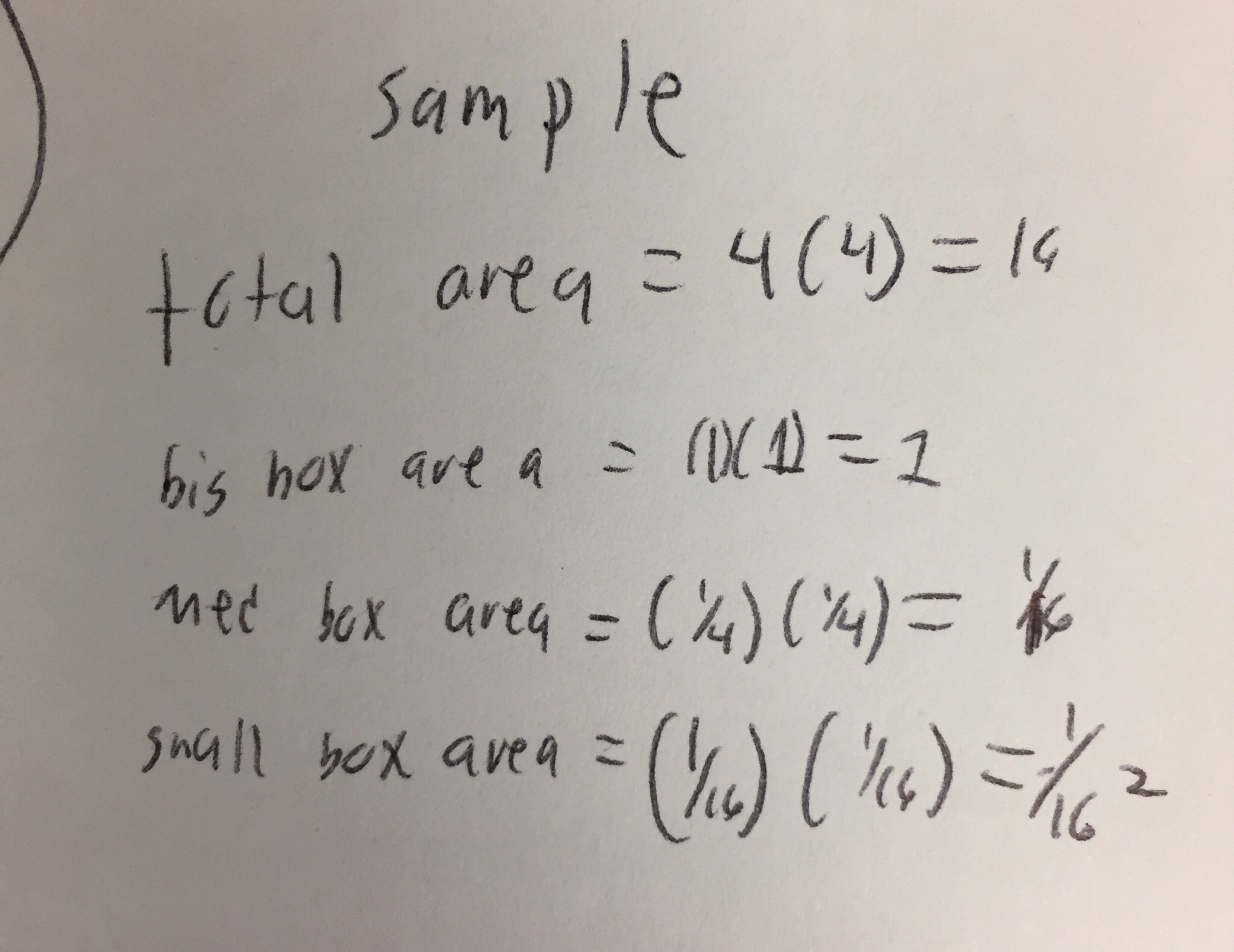
Now you know know some of the math, here are the calculations of all three levels. Pictures are included for level 2 & 3.
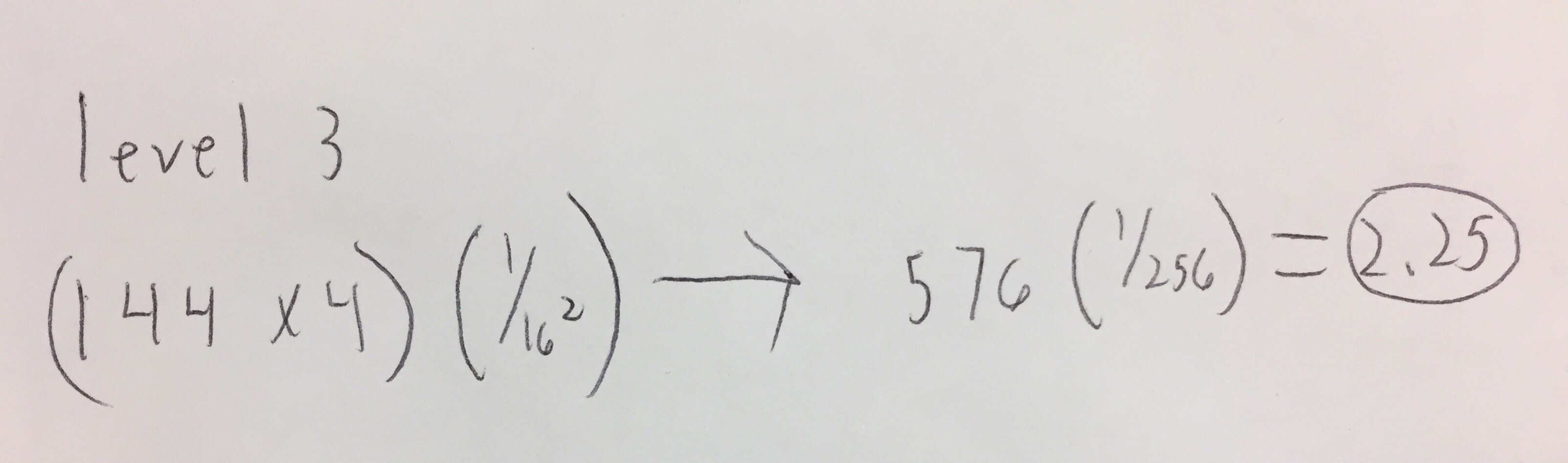
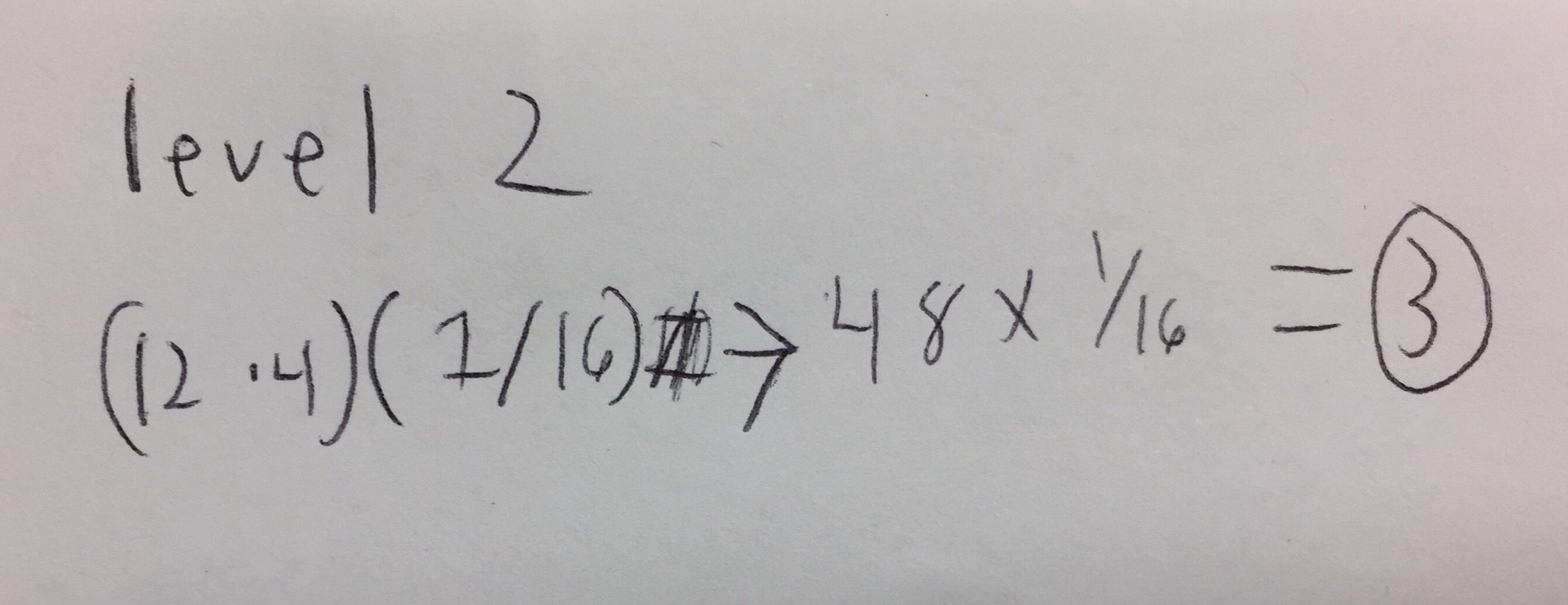
Level 1: (1 x 4) = 4
Level 2: (12 x 4) (1/16) = 48 x 1/16 = 3
Level 3: (144 x 4) (1/16^2) = (576 x 1/256) = 2.25
The following photo shows the total combined surface area at level 3.
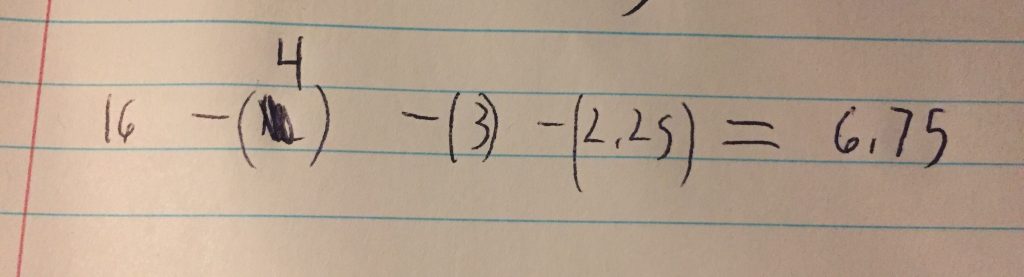
Calculating to Infinity
What would happen to infinity? Would there be a point where the fractal’s matter is too small to visually see? This picture will calculate the area if done at infinity. The strange part is the area is 0 because this fractal will constantly subtract matter until nothing remains.
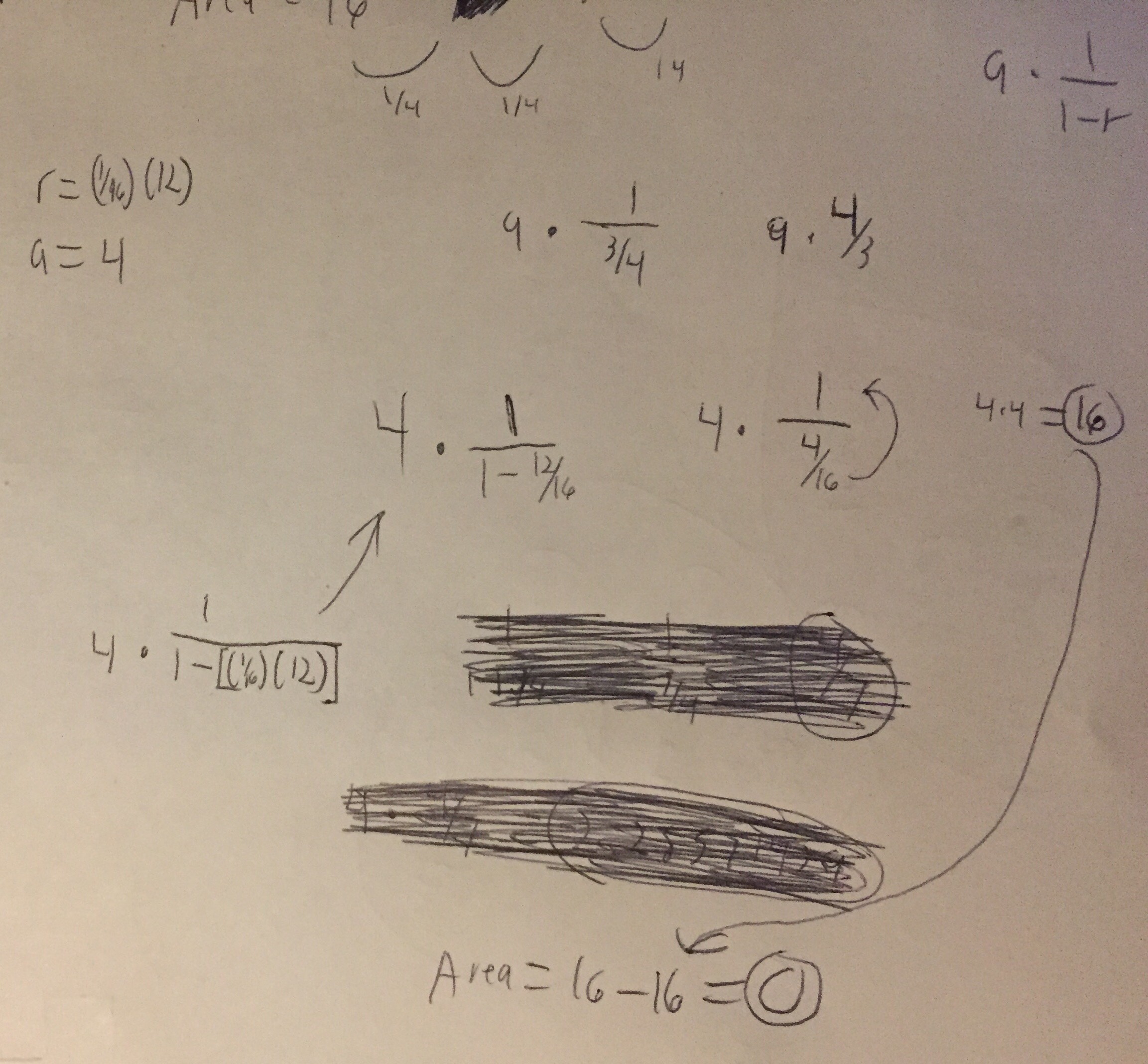
The formula for calculation is A x [_1_]
[1-r]
A = 4
R = (1/2)(12)
after simplifying the fraction portion of he formula, you end up with 4. Multiply that with A, which is also 4, to get 16. 16 is the initial area that a level 0 fractal carpet starts with, therefore, the area at infinity is 0.
Fractal Dimension
This will sound strange, the fractal carpet is neither 1-dimensional nor 2-dimensional. So what is it then? The fractal lies in between, but first it must be calculated. Look at the photo below and explanation.
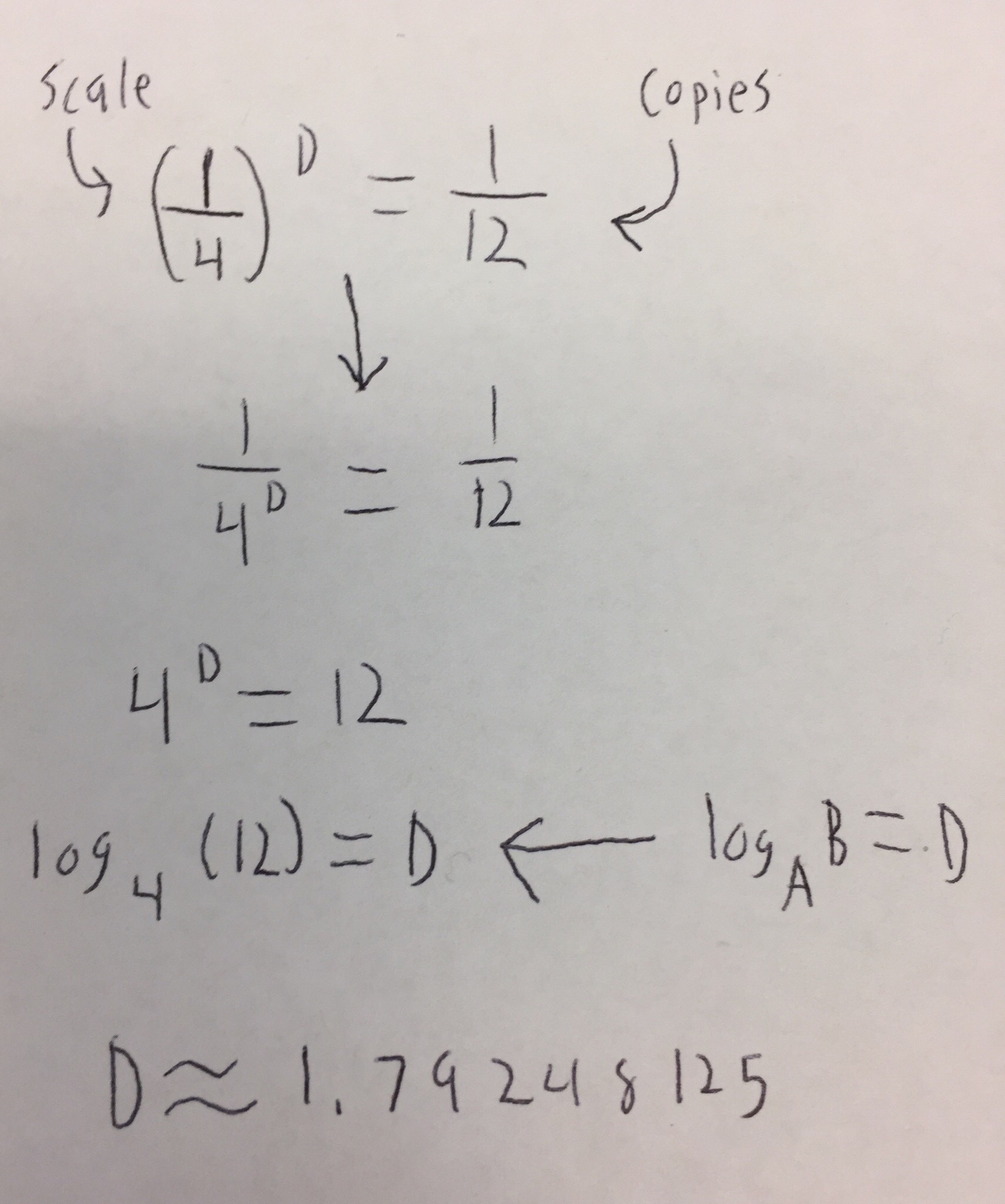
To start, you must know the numbers before the formula. The scale, the amount that each level divides by, is 1/4th for each new level. The amount of copies is the amount of squares remaining from a new iteration, consult the first level to see this. Using the logarithm, log base 4 of 12, we get this long number.
The dimension of this fractal is 1.79248125.
Download Link
You can find the code from this Thingiverse link.