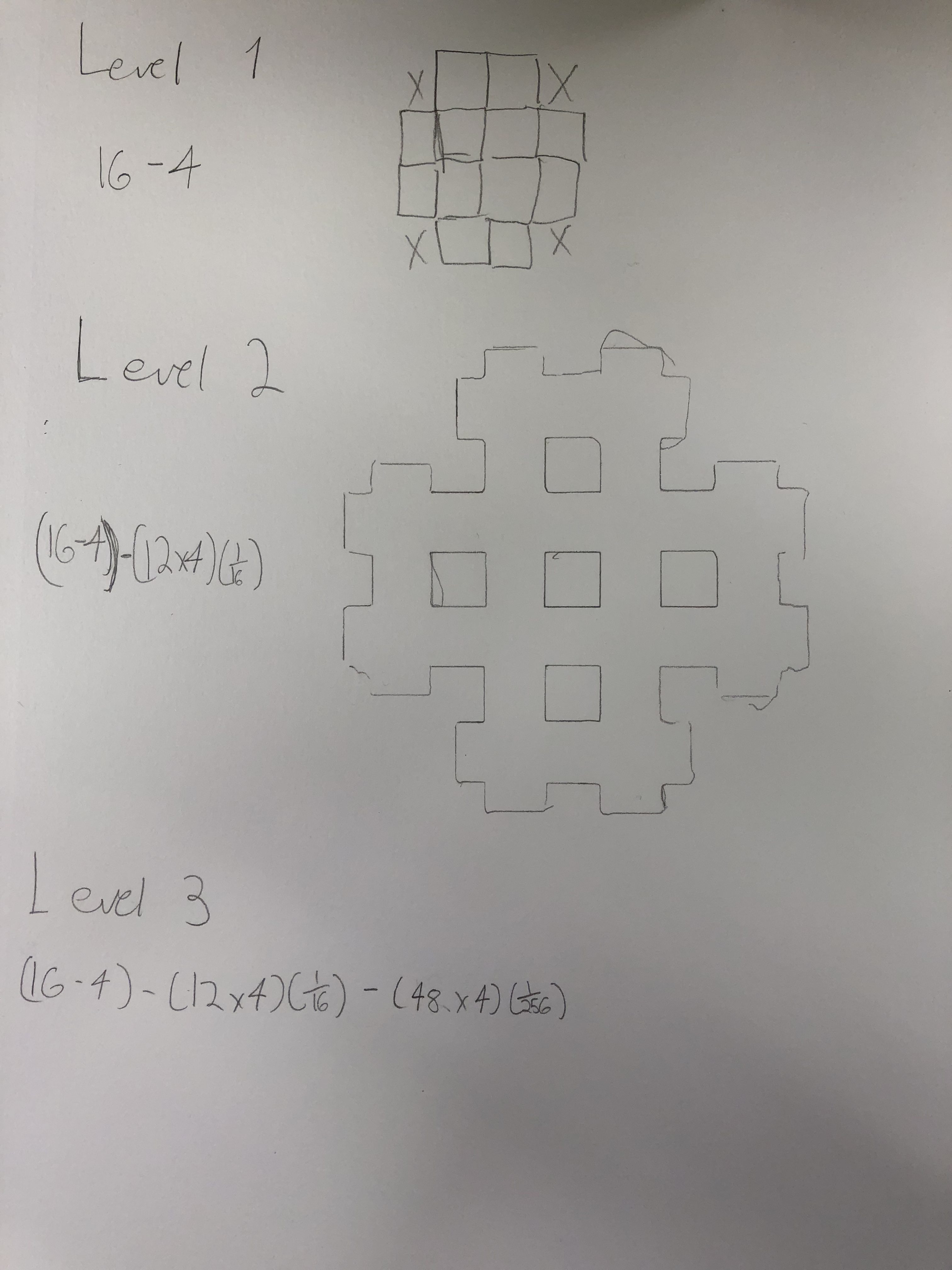
Level 1
To start with our carpet fractal, level 1 has 1 square removed from each of the corners creating a plus sign shape. When repeated for a level two, it creates a plus sign made of plus signs, and so on.
To find the area, I took the area of the original square and subtracted the area of the corner squares I removed. This gives us the area of our level one.
16-4=12
Level 2
Level 3
Next I removed 4 corner squares from each of the 12 remaining squares of level 1. That leaves us with our level 1 area minus 4 corners of the 12 squares in the level 2. This means we subtract the 4 corners 12 times, once for each for the remaining squares. We do this to subtract the 4 corner squares of the 12 left from level 1 but the squares we remove are smaller relative to the remaining squares from level 1.
(16-4)-(12*4)(1/16)
Basically imagine that one square from level one is another, smaller, level one, which is why we must multiply the area we subtract by 1/16.

Infinite Geometric Series Calculations
To find the infinite geometric series I used the geometric series equation a+ar^2+ar^2+ar^3…ar^n I calculated the infinite area of my fractal. Because r > 1 I used it in ax1/(1-r). Plugging the numbers in I got 4 x 1/(1-(12/16))=0 which you can further see simplified below. We take that answer and subtract it from the total area of the original square (16) so 16-16=0.
16 – [(4*1)+(4*12)(1/16)+(4)(12/16^2)+(4)(12/16^3)…..]
a/1-r
4 x 1/(1-(12/16))
4/(4/16)
4/(1/4)
4*4
16
The infinite series of the fractal is 0 meaning there is no area but still a possible perimeter.
Fractal Dimension
The fractal carpet is neither 1-dimensional nor 2-dimensional, as it is infinite. The fractal lies in between the 1st and 2nd dimension and must be calculated. We use the formula (scale-down factor)^(dimension) = 1/(number of copies)
To start every level is 1/4th for each next level. The amount of copies is the amount of squares remaining from a new iteration, look at the first level to see this. We then use the logarithm, log base 4 of 12.
The dimension of this fractal is 1.79248125.