For this fractal, I removed 3 squares out of the 16 that we started with. I removed a corner square, a square in the middle and one on the bottom row. The coordinates removed are (0,1), (1,2), and (3,3) To be able to calculate the area, we had to use a specific formula and apply it to the number of boxes removed in the fractal. The formula was 16- total # of big boxes- total #of a medium box- total # of a small box. The first level had 3 boxes taken out so I subtracted 16 minus 3 which gave me 13. In the second level, the medium box area was 1/16, so I multiplied the total of level one (13) by 3 and then by 1/16 and got 2.4375. Then applying the formula, I subtracted 16 by 3 and by 2.4375 and got the medium box total of 10.5625. For the third level, the small box area was 1/16^2 which is equal to 1/256. For this calculation, I had to multiply 13 (13)(3)(1/16^2). The answer I received was 1.98046875. When I applied the formula and did 16-3-2.4375-1.98046875, the total of the small box came out to be 8.58203125. These are the calculations of my fractal’s surface area:

As more boxes are added to each level, the lesser amount of surface area there will be after each iteration.
Infinite Geometric Series Calculations
These calculations were very difficult to calculate but when I figured it out, the calculations made sense. With the geometric series formula, a was equal to 3 and r is equal to 13/16. In my calculations below I learned that the answer to the formula a(1/1-r) with my calculations was equal to 16. By applying the formula, I multiplied 3 by 1/(1-13/16), which was then simplified to 3 times 1/(3/16) which gave me an answer of 16. I later subtracted 16 by 16 and got zero, which proves that my series is infinite through my calculations below.

Fractal Dimension Calculations
For the equation of the fractal dimensions, I had to solve a logarithm. The squares in my fractal were scaled down to 1/4. When looking at a smaller copy of the fractal, the larger one is 13 copies of the original fractal so the little square is 1/13 of the whole fractal. My calculations below explain the dimensions of my fractal. I used a logarithm to calculate the dimensions of the fractal which resulted in the answer of 1.85022. It starts out with 1/4^D equals 1/13. I then simplify it to 4^D equals 13. To make it a logarithm, the equation then becomes log4^13 equals D, resulting in D being 1.85022
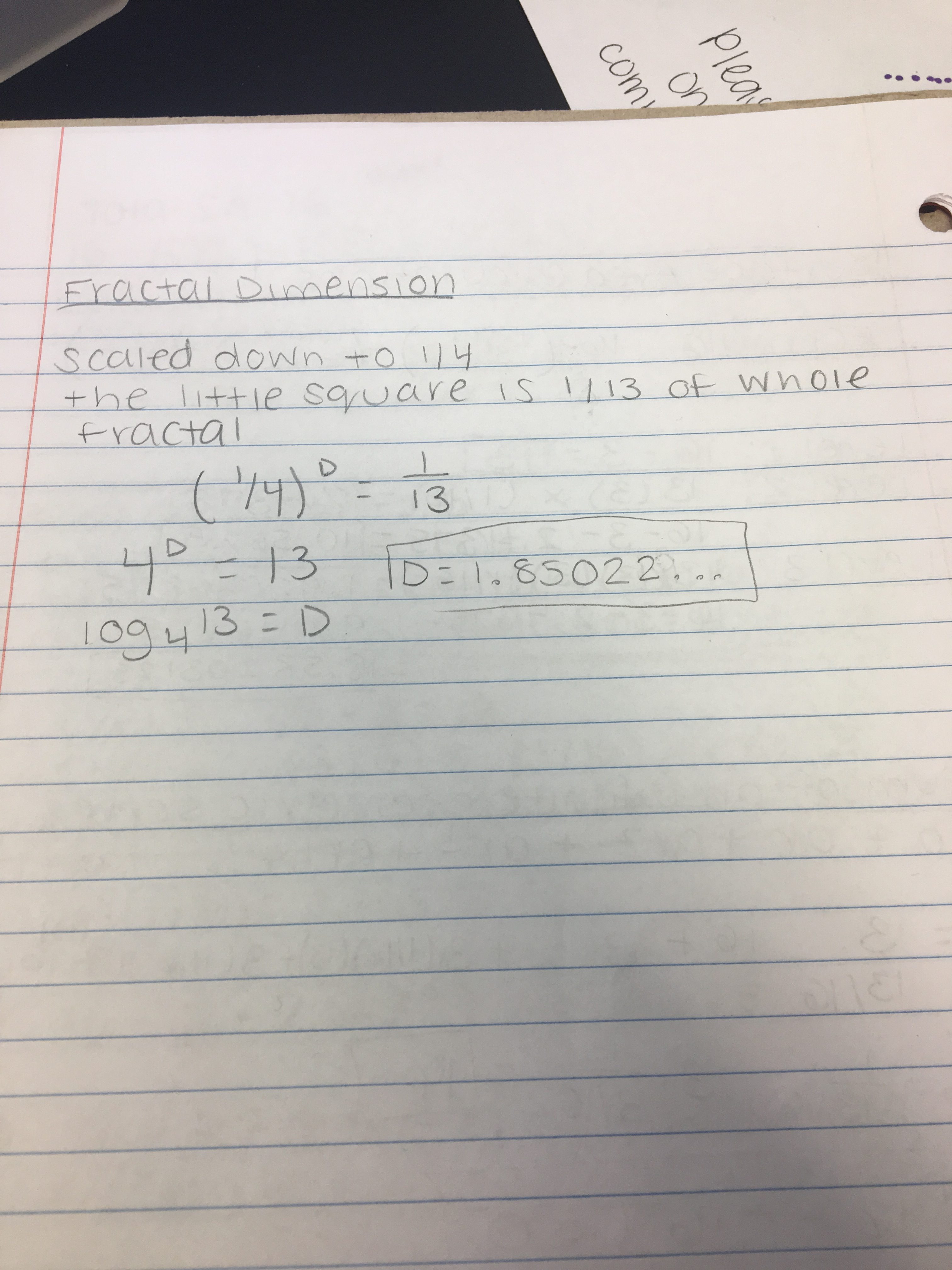
Level 1 Fractal

The surface area of the fractal is 13.
Level 2 Fractal

The surface area for the second level of this fractal is 10.5625.
Level 3 Fractal

The surface area of the third level of this fractal is 8.58203125.
Come check out my page on Thingiverse!