About My Fractal
Starting with 16 squares, I decided to remove 5; the four corner squares and a square on the inside. The coordinates removed are, (0,0), (4,0), (0,4), (4,4) and (1,1).

Below, you can see how the total area for each box level (total, big, medium and small) is calculated. This is important to know because it will be used in the formula to find the area for each iteration of the fractal.
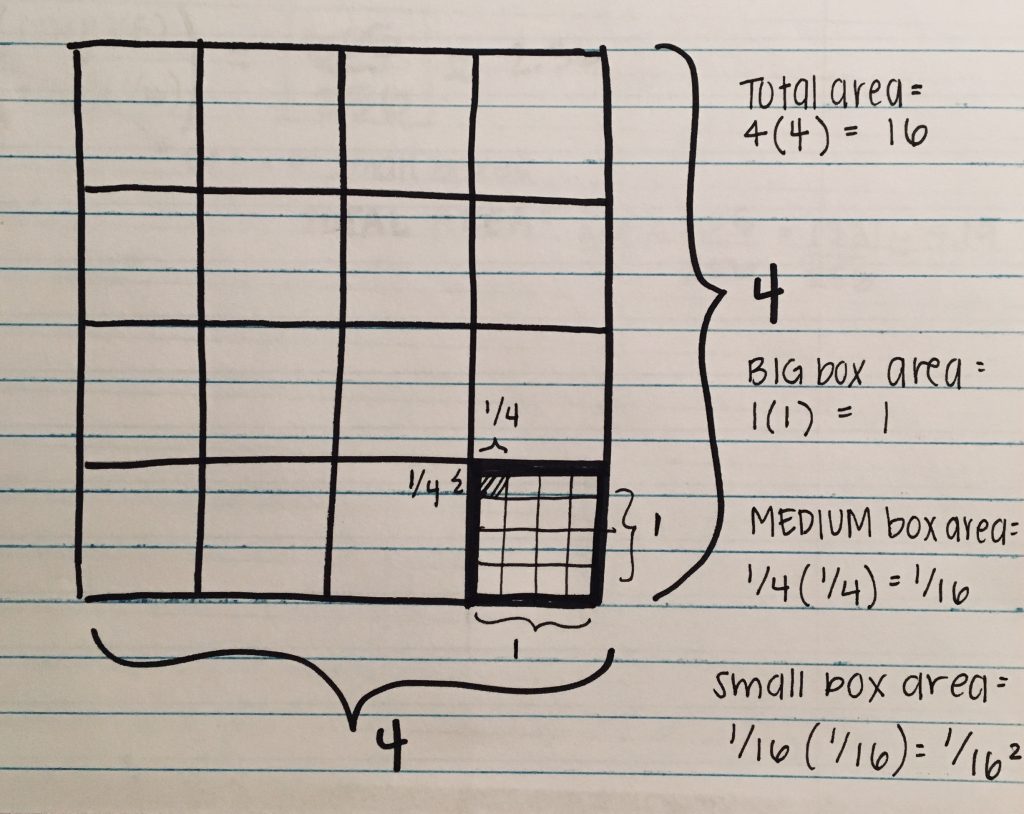
Crab Carpet Calculations
The image below shows the formula used to calculate the area for each iteration of the fractal.

Let’s break this image down a little bit starting from Level 0 (which is represented by the 16). Level 0 is untouched with 16 squares. For level 1, using the formula above, we take the initial number of squares and subtract the number of squares removed. 16-5=11, 11 is the area for level 1.
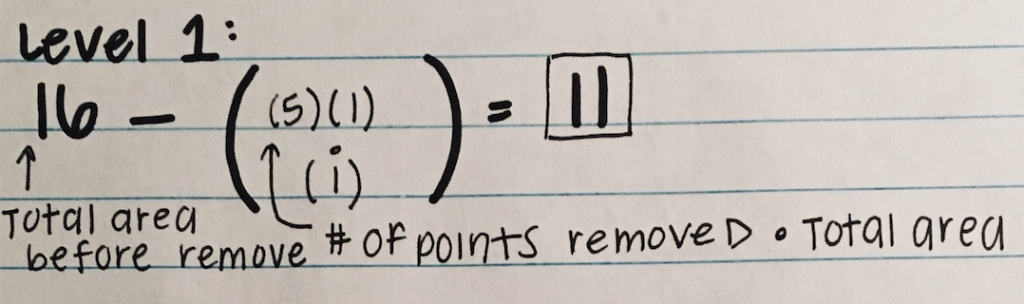

In level 2, 11 is how many squares are remaining from level 1. 5 represents the number of squares that will be removed again from each square. You then multiply (11)(5)(1/16), 1/16 being the area of the big sized boxes. You are then left with the area of level 2, 55/16 or 3.44. To find the total area of levels 1 & 2, you take the area from level one which is 11, and then subtract the area from level 2 from it. Therefore; 11-55/16= 121/16 or 7.56.


The calculations for level 3 are very similar. You start by following the same steps you did for levels 1 & 2. However, in level 3 you will multiply by an additional 11 because there are 11 more squares within each square. After multiplying, you are left with 605/256 or 2.36 which is the new area for level 3. To calculate the total area, you have to use your last total area which is 121/16 and subtract your level 3 area from that. Therefore; (121/16)-(605/256)= 1331/256 or 5.19.


Geometric Series & Sum Calculations
Key:
X= initial area
A= first term (consistent throughout series)
R= common ratio

Above is a formula for a geometric series. This formula shows a pattern, how the fractal works or is repeated. X is the initial area, A is the number of boxes removed from each square and R is a constant that is calculated by first subtracting X-A then multiplying that number by the area of each box, 1/16. The image below demonstrates how the fractal works with the formula up to the third iteration.
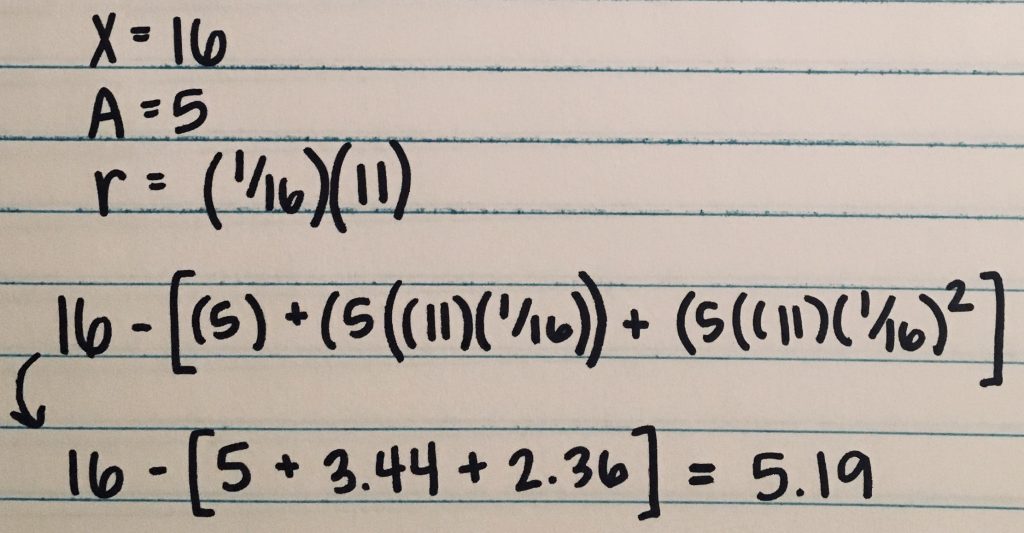
Key:
a= how many pieces were first removed
r=common ratio
To calculate the sum, you would use a different formula. The formula is A * 1/1-r. After calculating the math shown in the picture below, you can see that the sum or total area of this fractal at infinity is 0.

Dimension Calculation

There are multiple steps to solving for the dimension of a fractal. First, you need to know the scaled-down factor, which is how much the original fractal was getting smaller by. Starting with a scale of 4, in level one, the fractal was cut into 16 pieces with each square being 1×1. Then each square was cut again, leaving the scaled-down factor to be 1/4. Now, you have to know the number of copies scaled down, which for this fractal is 11, since 5 pieces were removed from 16.
Now that you have the scaling down factor, 1/4, and the number of copies after initial removal, 11, the last step is to use the dimension formula, which is A^D=B. A represents the linear scale, the original scale of 4 and the smallest square scaled down, which is 1/4. D is the dimension, what you are solving for, and B is the number of copies remaining after initial removal, 16-5=11 or 1/11. After plugging these numbers into the formula, you can see that the dimension of the Crab Carpet Fractal is 1.729.
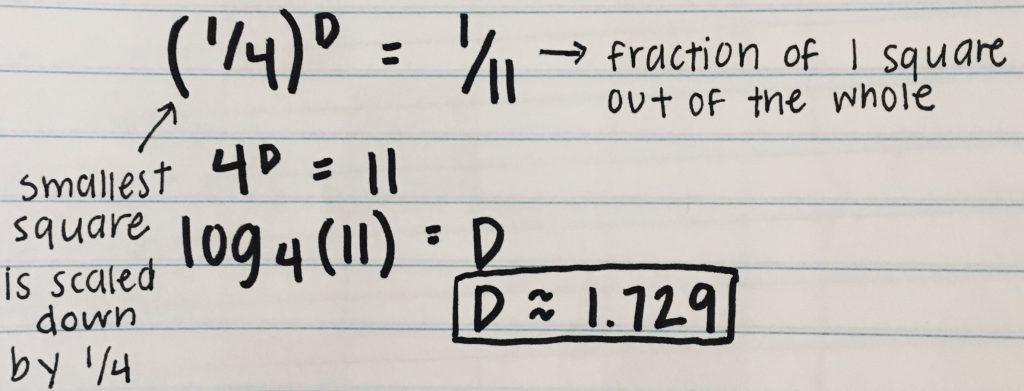
You can find my fractal on Thingiverse here.