

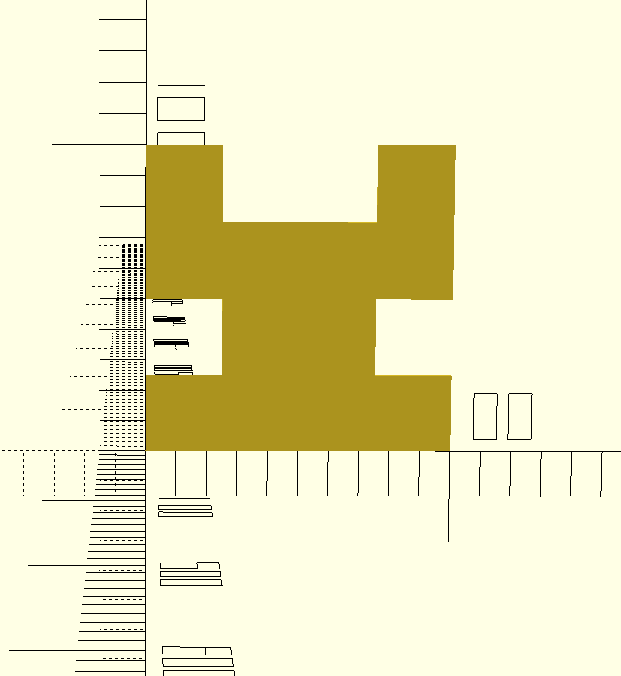
When I created my fractal carpet, I removed squares: [0,1] [3,1 ] [1,3] [2,3]. I named my fractal the Fork Fractal because of the way that it splits off into two at the top. When the design moves up a level, it creates more little splits within the large one show in level 1. I thought that removing these squares created an interesting design because two of the squares combined to make a rectangle.
Surface Area Math:
Below I have included the step by step processes I completed to get the surface area of my fractal, and to apply it to the infinite geometric series.

After I calculated the surface area, I had to break it down and apply it to the infinite geometric series formula. When you put one on top of the other, you can start to match up the pieces and input numbers into “a” and “r”.

If you look at the piece of explanation I added to the right of the formulas, you can see where the (12/16)^2 came from. In the surface area formula, both the size of the boxes and the number of times the boxes were taken out increased infinitely. Because of this, both had to be represented by “r” in the formula.

Infinite Geometric Series Math:
When it came to applying the infinite geometric series formula we have been learning about it class, I simply plugged in the values of “a” and “r” and solved. 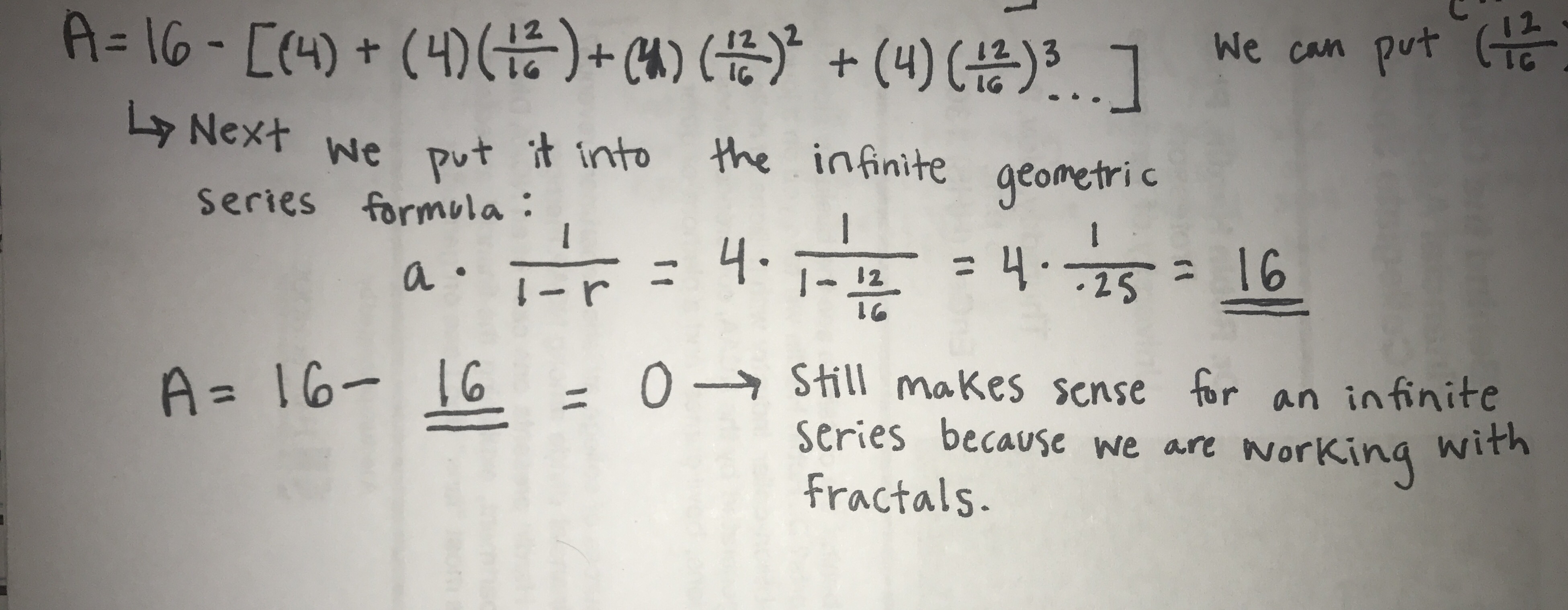
While it may seem impossible to have an area of zero, the infinite removal of squares in the fractal pattern is what makes this possible. In an infinite series, the area will be zero yet the fractal will still not be empty. On my fractal, two of the very corner pieces will always be there, they will just be so minuscule their area will not have any numerical significance.
Dimension Math
When it is scaled down by 1/4, 12 copies of the whole fractal are made. I broke down this math into the demonstration below. As you can see, when my fractal was repeated to level 2, the initial 4 squares that I removed were no longer involved in dimension calculations. This is shown by the four squares that are entirely shaded out.

Next, this information is applied to the dimensional analysis equation. 
The dimension of my fractal is 1.792.
Sharing
I uploaded my design to Thingiverse, which can be viewed here!