The Railroad Track Carpet design was made by removing four blocks from level 1 with the coordinates [0,1], [3,1], [0,2], and [3,2].
Using the equation shown below we can calculate the surface area of each level even as the complexity of the design increases with each iteration of the fractal. I will be calculating levels 1, 2, and 3 for the Railroad Track Carpet fractal.
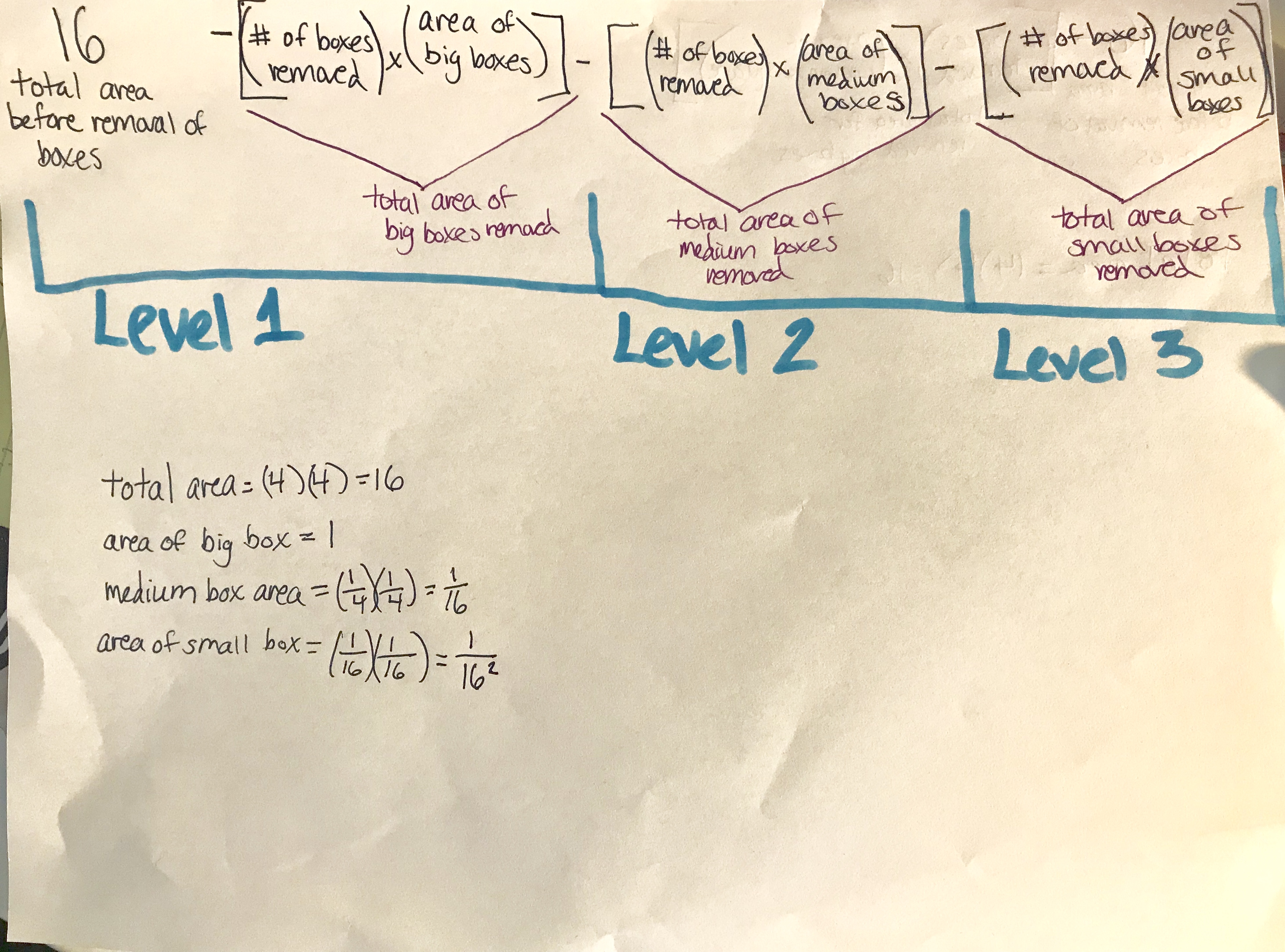
Level 1

The surface area for level 1 would be the number of boxes removed, (4), times the area of the big boxes, (1), from the number of boxes that comprise the total area of the complete square, (16). Therefore the equation would look like 16 – [(4)(1)]=12, so there is a surface area of 12 units.
Here you can see the calculations.
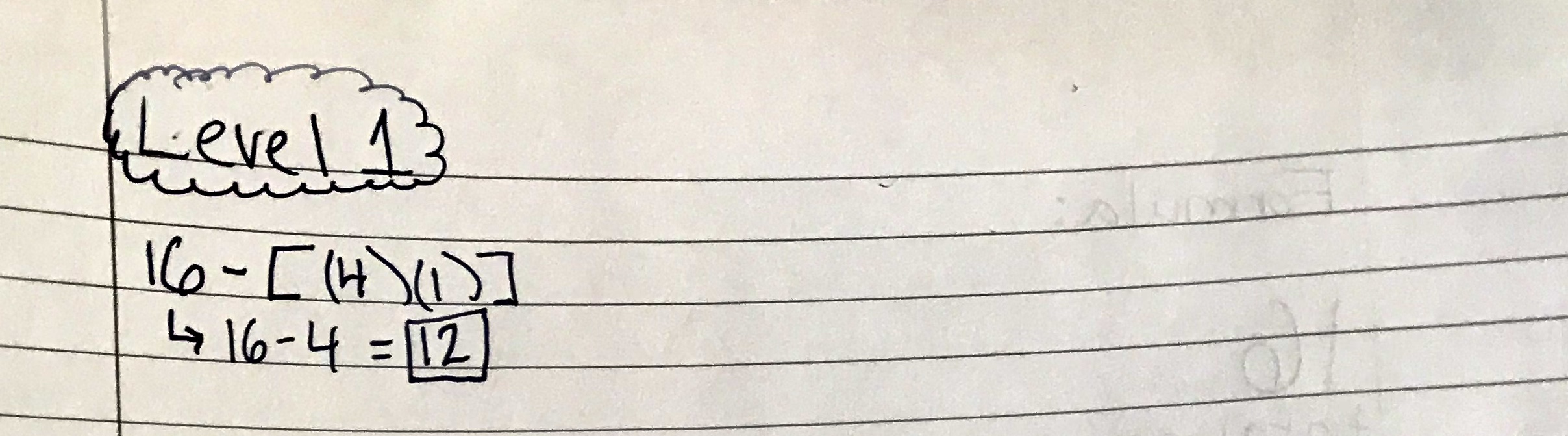
Below shows how the 4 empty squares of the grid represent the 4 squares removed from the 16 total squares. Each square in the grid, or “big box”, is one unit, as shown in the equation above.

Level 2

For the level 2 Railroad Track Carpet we are going to find the area by finding the sum of the total of the number of removed boxes (4) x the surface area of the medium boxes (1/16) x the number of times 4 boxes were removed (12). This sum would be subtracted by the level 1 portion of the formula, so the equation would be 16 – [(4)(1)] – [(4)(1/16)(12)]. However, we want to put this equation into geometric series format, so we will simplify (1/16)(12) into 12/16 by using the laws of basic algebra. 12/16 is the r value of the geometric series variables ar, while the a value is 4.
Now the calculations will look like 16 – [(4)(1)] – [(4)(12/16)]=9.

Since we simplified the equation and found that our constant r-value is 12/16 I will now use only that in the geometric series equations of the other levels.
Below is a visual that helps in seeing how I have removed 4 boxes from each complete fractal. You are able to see smaller versions of the level 1 stage of the fractal in 12 out of the 16 squares. So therefore I removed 4 boxes, 12 times. In each level this pattern will continue but be squared.

Level 3

For the level 3 Railroad Track Carpet we are going to find the surface area by subtracting the total of the number of removed boxes (4) x the surface area of the small boxes (12/16)^2. Since this is another iteration of the fractal we are raising the r value to the number of iterations of this level. We subtract that sum from our previous area for level 2.
So the equation would be 16- [(4)(1)] – [(4)(1/16)] – [(4)(12/16]=6.75.
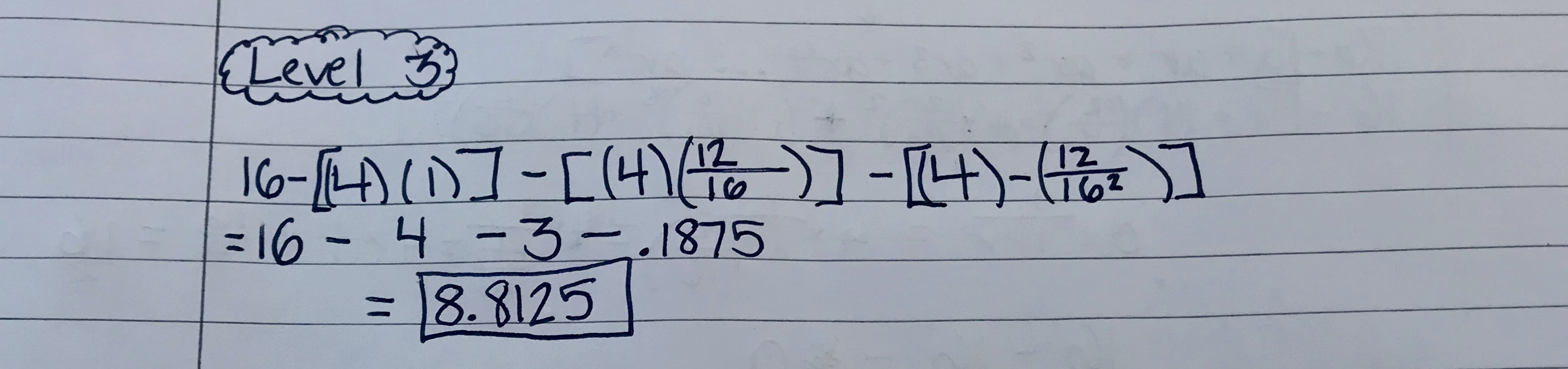
With the second level of the fractal I had removed 4 boxes from the square 12 times. With the third level of the fractal I have now removed 4 boxes, 12 times, 12 more times. Which is why (12/16) is squared in the equation—> (12/16)^2.
Level 4
Infinite Geometric Series Calculations
Using the geometric series equation of a+ar^2+ar^2+ar^3…ar^n I will calculate the infinite surface area of the railroad track fractal. Since the r-value (12/16) is less than 1 we plug it into the equation a x 1/(1-r). Plugging the values into the equation the calculation comes to 4 x 1/(1-(12/16))=0 which you can further see simplified below. We take that answer and subtract it from the total area of the original square (16) so 16-16=0.
The infinite series of the railroad track fractal is zero which is very unique since one would think the fractal would continue until it no longer exists, but it still exists even when the surface area is at zero.

Dimension Calculations
To find the dimension of the Railroad Track Fractal I will use the formula (scale-down factor)^(dimension) = 1/(number of copies). The factor for how much the fractal will scale-down with each level is 1/4th. The number of copies is 12 because as was illustrated in the pictures and represented in the surface area calculations, the pattern is replicated 12 times more in each iteration.
Before I fully calculate the dimension let’s look again at the level 2 iteration of the fractal. You can see how there are 12 complete copies of the fractal in the 16 box grid. There will be more 12 more copies of the fractal for each complete fractal with every iteration which is why 12 is the number of copies in the dimension calculations.
The level 1 iteration of the fractal showed 12 remaining boxes out of the 16 of the original square makes the fractal look like an “I”. You can see from the level 2 print below how the width of the original “I” is scaled down by 4 boxes and the height is also scaled down by 4 boxes so that the original “I” of the level 1 fractal fits into one box. That is why the scale-down factor for the dimension calculations will be 1/4th.

Pictured here is the dimension calculations. 
Thingiverse
Make it yourself by finding the files in Thingiverse!
