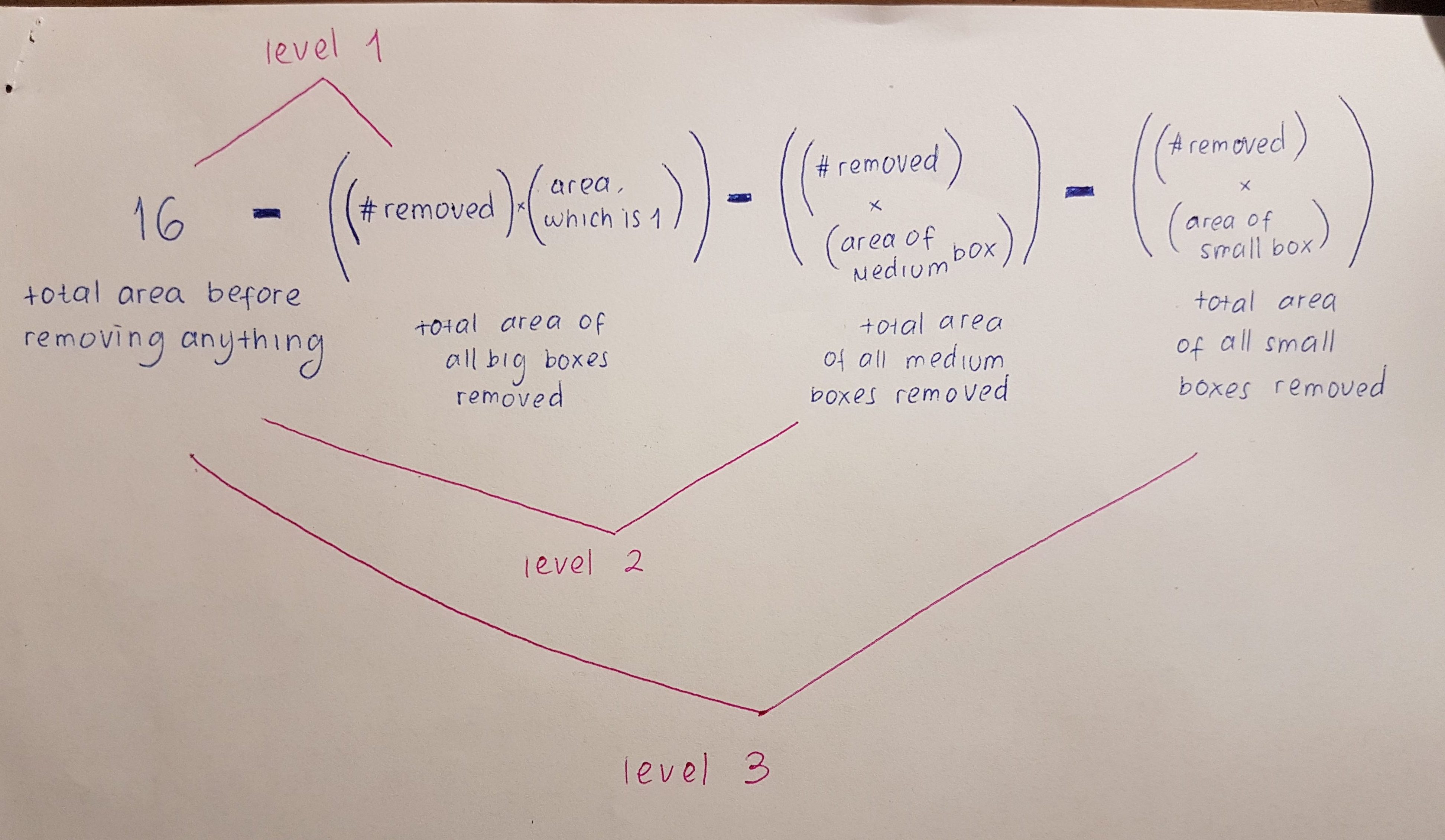
Tetris Carpet Fractal
For this particular carpet fractal, I removed three sections (boxes) that are towards the middle of the square which are (2,1) (1,2) and (2,2) in order to create the first level of the fractal. The reason why I removed these sections was because I thought the fractal was unique and removing three points would make a more unique fractal with an “L” shape.
Level 1

In order to calculate the surface area of the fractal, I did the following:

For the first level, I simply subtracted three from sixteen, since there are three boxes that are removed from the fractal and the length of each side of the whole big box is four. So basically the area of one of the boxes I removed is 1 because it is basically 1/4 the size of the biggest box.
Level 2

It would be easier to see the fractal if we used a grid in order to see the individual boxes and it would certainly help with calculating the surface area. Therefore, below is a picture of the 2nd level fractal with a grid.

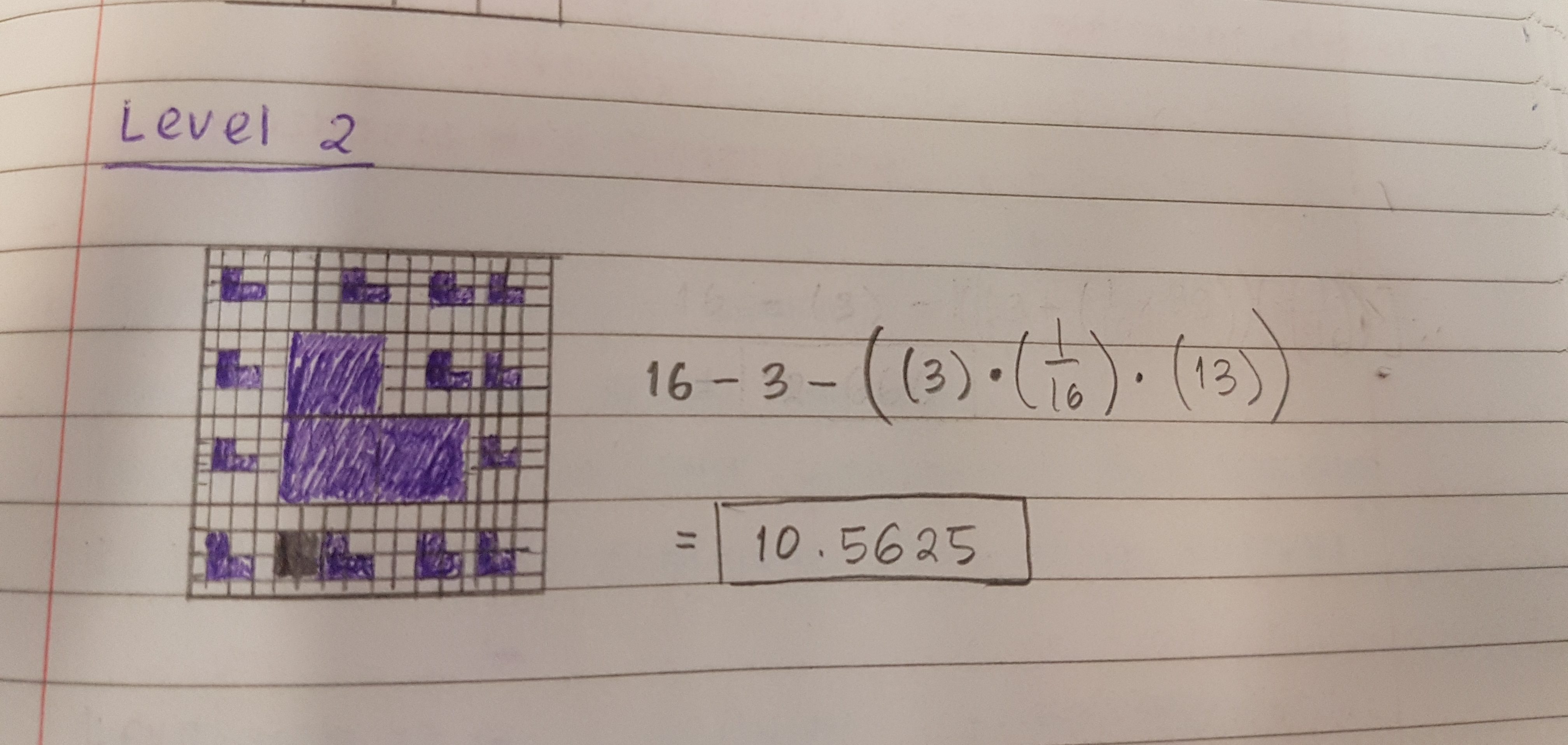
For Level 2, I would need to multiply 1/16 by three since 1/16 is the are of the medium box. I got it by multiplying the length of the medium box, which is 1/4 by 1/4. Afterwards, I multiplied that result by thirteen because when I count it manually there are 13 sections for the medium boxes that the smaller boxes are taken out.
Level 3


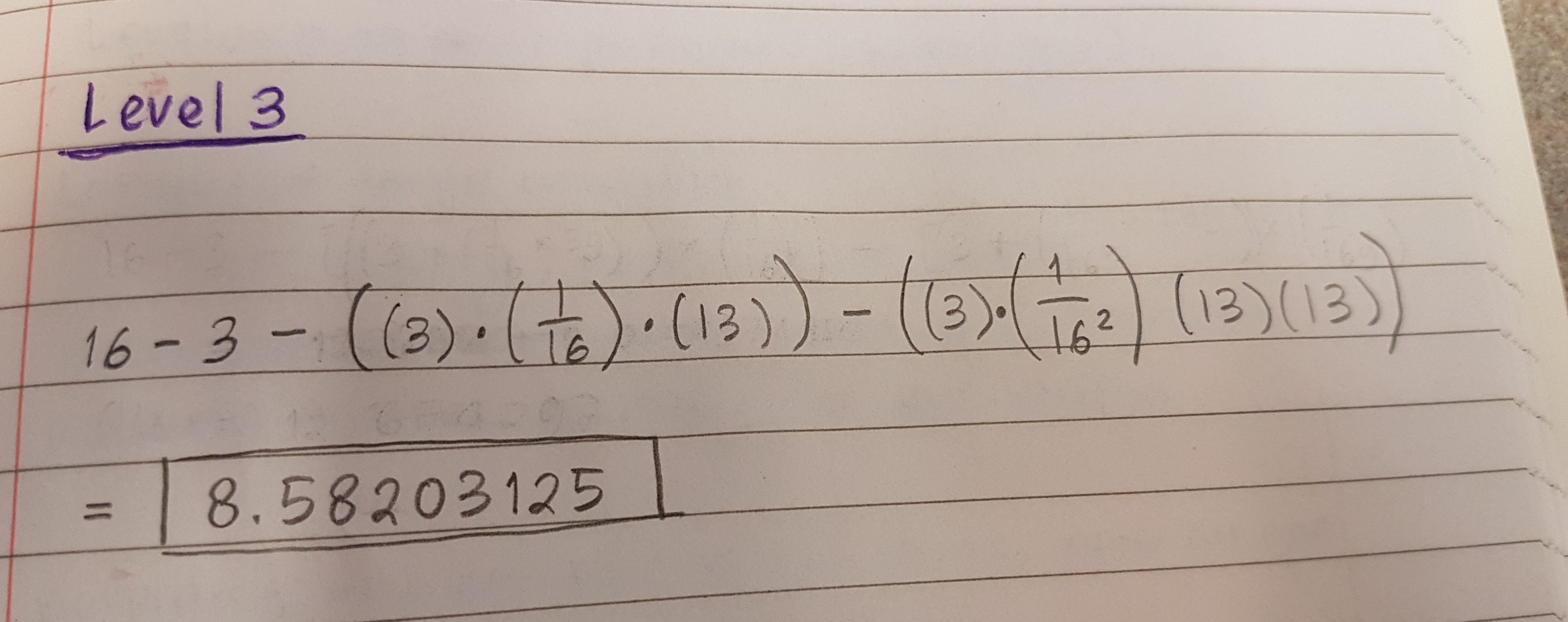
Calculating level three can be a little bit more complex, however I simply need to decrease the area of level two by the small box area multiplied by three (boxes removed) and also multiplied by thirteen squared since there are thirteen more sections removed.
Level 4
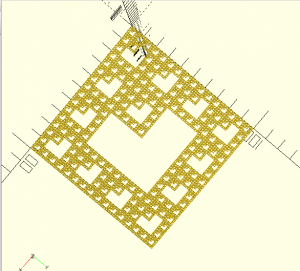
Infinite Geometric Calculations
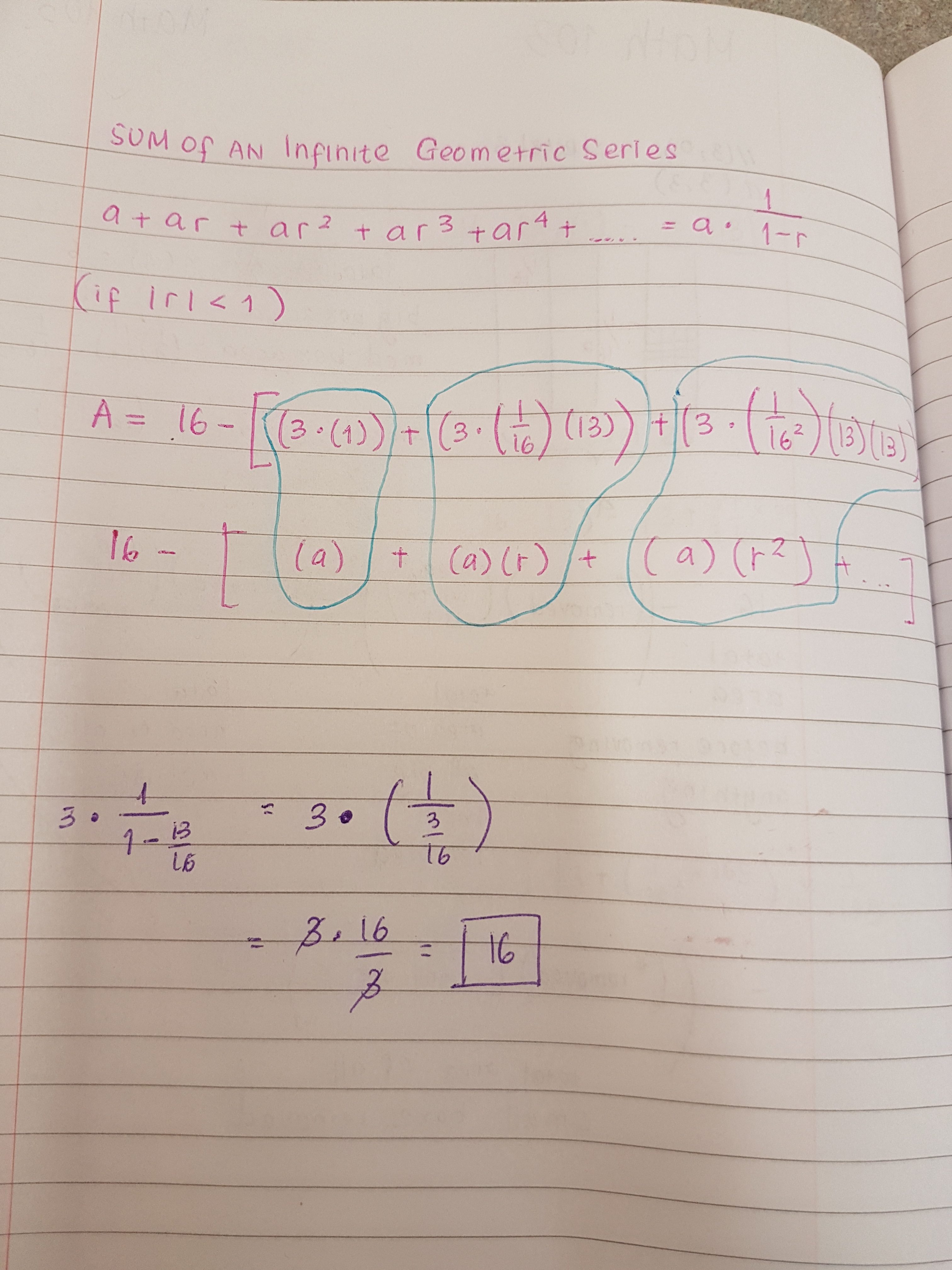
The calculation with the purple ink shows only the one within the brackets. Since I got 16 as the result of the calculations within the brackets, I then need to subtract 16 from 16 (16-16) resulting in ZERO. Therefore the sum of the infinite series of my fractal is zero which is very interesting since it will have a surface area of zero, yet it does not cease to exist and the fractal is still there.
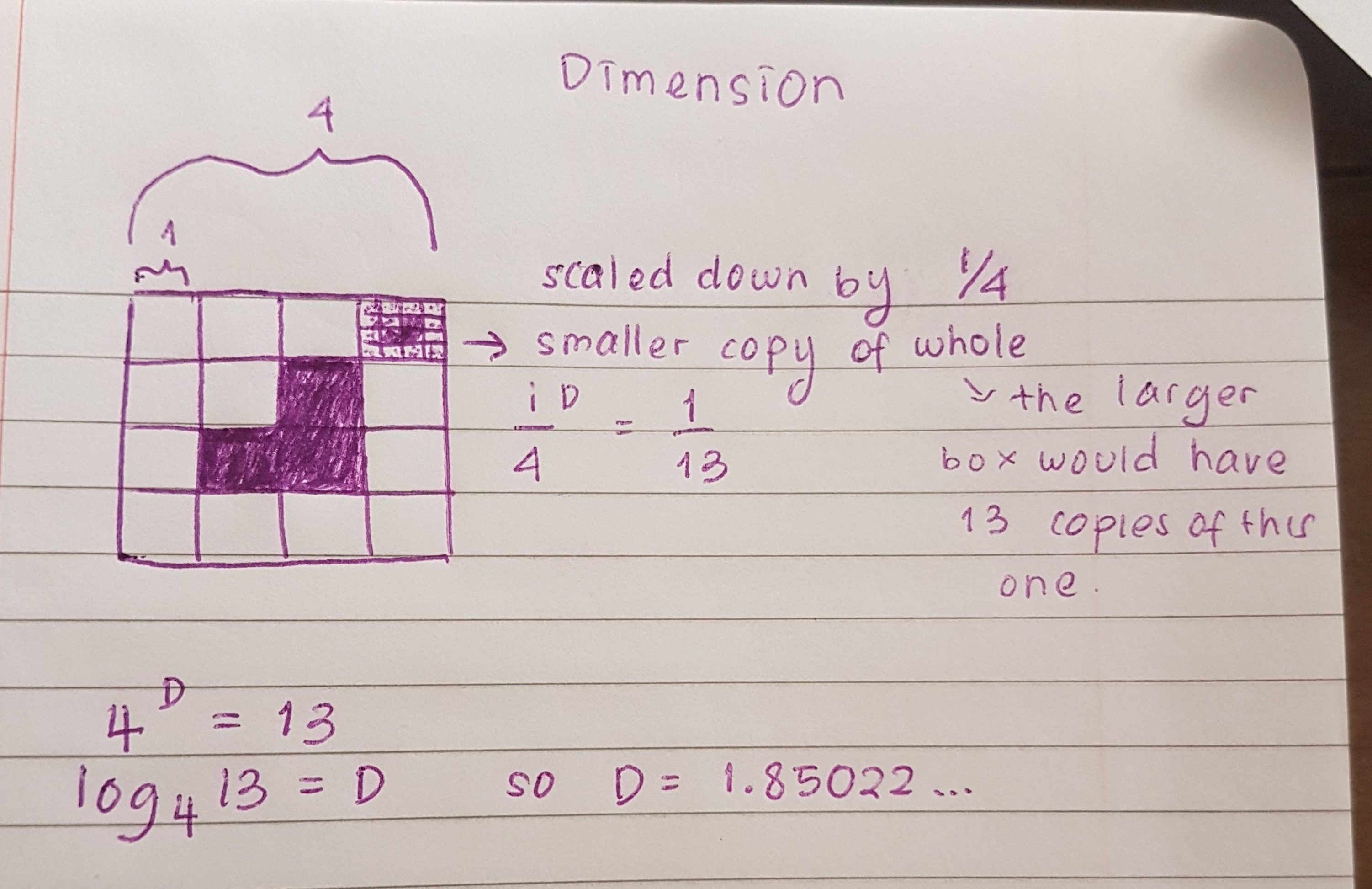
Fractal Dimension
In order to find and calculate the dimension of the tetris carpet fractal when it goes to infinity, we first need to figure out how the fractal is scaled down. We know that it originates from one big box and then then it is divided into four smaller boxes, meaning that the linear scaling factor would be one fourth.
Thingiverse
In case you are interested in seeing the fractal model on Thingiverse, please click the link below!