Koch Snowflake

The first fractal I want to print is the Koch Snowflake. According to Wikipedia, the Koch Snowflake is a mathematical curve and one of the earliest fractal curves to have been described. It is based on the Koch Curve which appeared in a 1904 paper titled “On a continuous curve without tangents, constructible from elementary geometry”. The progression for the area of the snowflake converges to 8/5 times the area of the original triangle, while the progression for the snowflake’s perimeter diverges to infinity. Here’s an illustration from the same Wikipedia page article where you can see the repeating pattern of the Koch Snowflake.

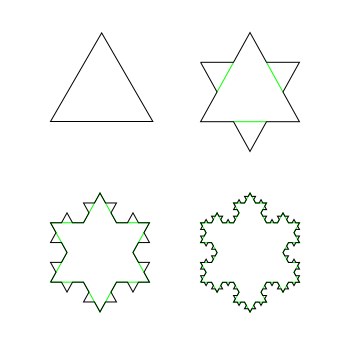
This Khan Academy video goes into depth about the Koch Snowflake’s perimeter, area, and volume. They say this a shape that has an infinite perimeter but finite area. The thing I found interesting about the Koch Snowflake was that it looks the same or very similar at any scale you look at it.

I think I could successfully print the Koch Snowflake. This model was designed by SimonFront on Thingiverse. I think it is printable because the scale of the fractal is simple but shows the basic idea of the fractal.

3D Printing Results

After a few misprints, my group finally each had a fractal. For my Koch Snowflake I ended up having to choose a different model off of Thingiverse due to the previous model not having the correct files needed to work in the two 3D printers we’re using in class. Although after having to repeat the process a couple times, I became a lot more aware of how to use the software the correct way. We ended up talking about the Koch Snowflake in a discussion in class and went in to depth about the Snowflakes finite area with an infinite perimeter.