Group Members
Emily Clark (Designer)
Taylor Zabinsky (Math Consultant)
Grant Folsom (Editor)
First Design Iteration
The repetition is by half the dimensions of the previous base. (Ex: Base 3 is half the length, width, and height of Base 2). Each increased base is then halted and so on. This makes it a fractal because it is a duplicate and a scaled down version of each base.
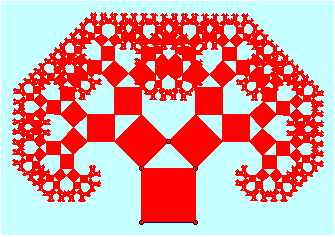
We originally wanted the design to stack on top of the previous stages instead of extending them to the base. The final print was extended to the bottom for support, but it maintains the original look when viewing this at the top. The image in Tinkercad had six stages in total. because this design has no complicated designs and rather blocky, the print should be relatively easy. This design sent to the printer is slightly scaled down due to time constraints, but a full model is possible given the whole length of the class.
3D Print Results
The resulting print almost copied the concept from Tinkercad. The only thing missing in the final print was the sixth level was too small to print, so it is not show in the image.

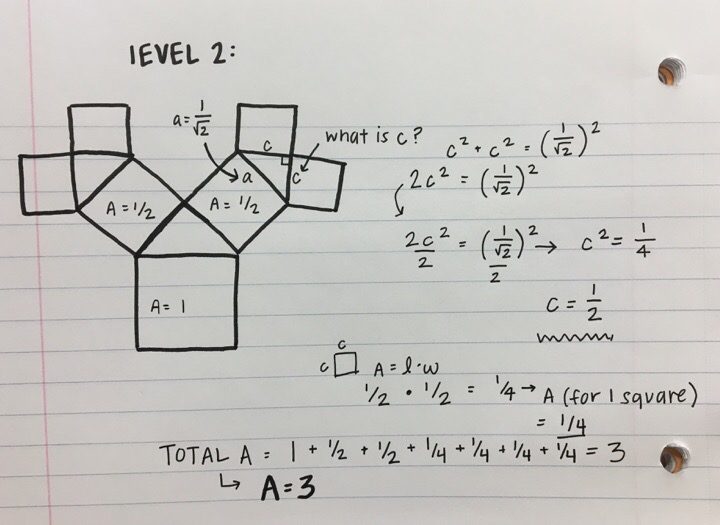
Area Calculations
The math for the fractal we designed would have been difficult to compute due to the overlapping areas. We chose to look further into Taylor’s fractal, the Pythagoras tree, because we thought it could be interesting. We decided to solve for area using the pythagorean theorem. The area for level 0 is 1. We discovered that each new square that is added, is sized down by 1/2 of the previous square. So for each new iteration, the total area is increased by 1. If you continue the math for each iteration, you will learn that the area for this fractal is infinite.
Level: Area:
0 ————– 1
1 ————– 2
2 ————– 3
3 ————– 4
4 ————– 5
100 ———- 101
n ————- n+1
∞ ———— ∞+1
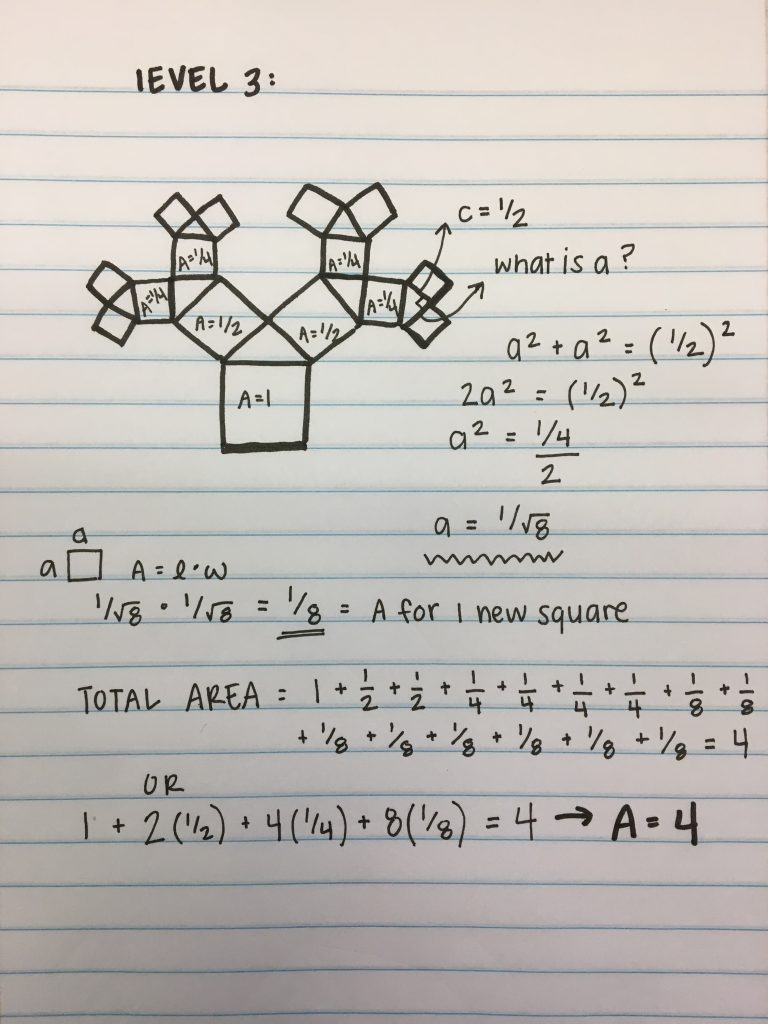
Fractal Dimension

We could not compute the fractal dimension as the multiple layers are stacked within each other, making the fractal too difficult to calculate.
The fractal used to for calculations is the Sierpinski Carpet, a link is found here. The equation for this dimension log 8/log 3 which is approximately 1.892789260…
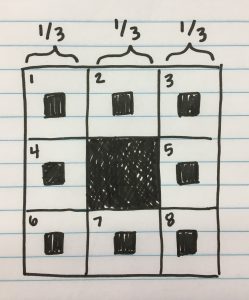
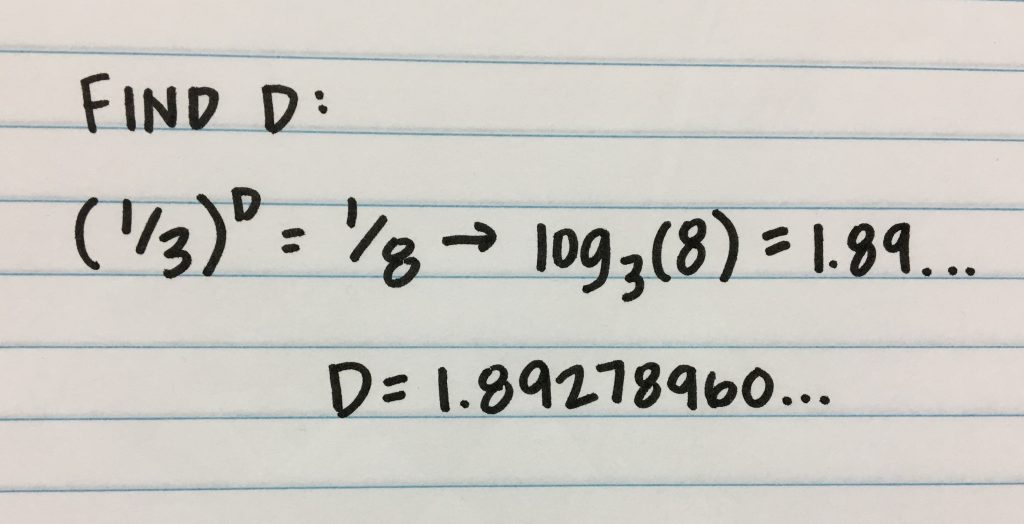
We chose to measure the dimension of the Sierpinski Carpet because the fractal can be calculated within in both a 2D or a 3D plane. Our other fractal would require calculations on the x, y, and z plane as a whole.
An external link with visual images can be found here for more information.
How to Find Our Models
Whirly Cross: Thingiverse & Tinkercad
Pythagoras Tree: Thingiverse
Sierpinski Carpet: Thingiverse

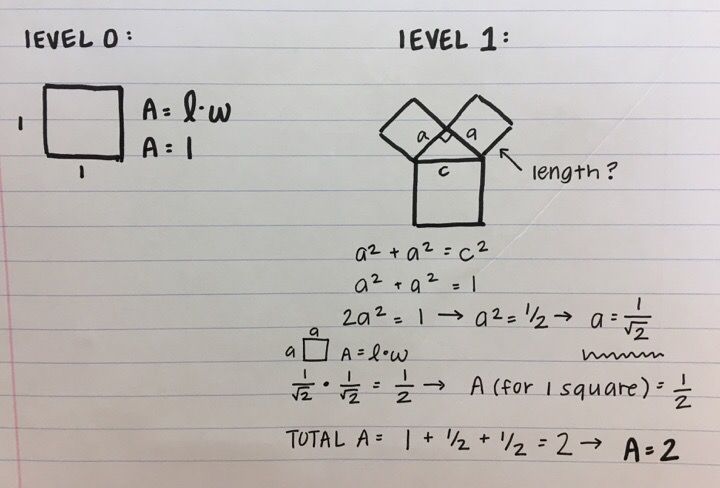
I like your use of handwritten screenshots. Can you make your images full size please?
Also I wouldn’t say “disapproval of its appearance”… what was the reason the first design might have been difficult to print?