Group Members:
Michael Conway (Designer)
Michael Mathis (Math Consultant)
Hunter Simmons (Writer)
Project Idea:

Our initial project idea is to create a Meissner tetrahedron. It involves taking a regular triangular tetrahedron, but then rounding all the parts to a precise point creates the Meissner Tetrahedron. What is really cool about this is that, although it is not like a circle containing zero edges and completely smooth, it will function in the same way as a circle if you were to use it by rolling a plane on top of it. Just like the circle, there will not be any bumps; only a smooth ride. If we are able to create the Meissner Tetrahedron in a timely manner, we would then like to use that figure to go deeper and then try to create a lemon juicer where the tetrahedron is used as the top part of the juicer and have a sphere or two placed underneath to catch the lemon juice.
First Steps:
We have learned that the Meissner Tetrahedron is definitely not as simple as it looks. The mathematical equations based around the tetrahedron are very complex, so we are trying to dig and find more information about the makeup of the design equations. For this we found a very helpful video that we hope to pull vital information from giving us a better sense of direction on how to do the calculations. This video is found here by Numberphile.
During class we decided to see what our design will actually look like in reality, so we decided to print one of the Tetrahedrons we had found on thingiverse to help in the design phase. We found the highest rated by likes and actual makes and decided to test it out. Surprisingly enough we had 2 unsuccessful prints, which we have yet to understand why they actual were not successful. The print wanted kept leaving a huge gash on one side which would ultimately lead to it splitting in half each time. We tried different sizes of prints both ending up in the same results. Hopefully next class we can potentially try using a different printer to see if that is the ultimate problem that keeps occurring. Here are some pictures of our unsuccessful prints.


Design Process:
Since our design has been complicated to make, instead of using Tinkercad, we have decided to use a different program called AutoDesk Fusion 360. In order to get the equal rounded sides on the design, you initially have to start with a basic triangle while adding in 3 separate circles ultimately becoming half spheres to each side and grouping will ultimately pull the sides out to a rounded sphere like triangle which is ultimately the final design of the Meissner Tetrahedron. Since the design was so complex we had to follow a tutorial in order to help understand the software as well as how to make the design. If you want more detail you can watch and follow the tutorial here.
Final Print of the Meissner Tetrahedron:

Final Prints in action:
As you can see, the book stays at a constant level rather than jumping up and down like you would think would actually happen.
This ultimately isn’t our design because we found out that the program which we were trying to create the Meissner Tetrahedron was much harder than expected. Even by following videos and tutorials on how to run Fusion, it ultimately ended up being a failure when trying to group and ungroup different levels of the design. The pictures on the right are the point that we made it to in creating the Meissner Tetrahedron, but after this point we ran into problems with the Fusion software.
Mathematics of the Meissner Tetrahedron:
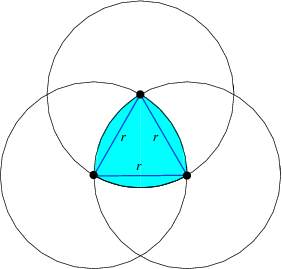
A relatively fluent rolling object doesn’t always have to a sphere, a sphere is just one of many different options. As shown in the video, the Reuleaux Triangle is one those options.
The Reuleaux Triangle was named and created by Franz Reuleaux who is also the father of modern kinematics. A Reuleaux triangle is a shape formed from the intersection of three circular disks, each having its center on the boundary of the other two. It is considered a cousin of the Meissner tetrahedron. They are both similar mathematically and conceptually, except that the Reuleaux Triangle is two dimensional, and has less rounded edges.

There are two possible arrangements for this replacement. Three modified edges can be placed around one face, or three modified edges can meet at a vertex as shown in the images above. Both of these arrangements satisfy the condition that opposite pairs of edges are always of different type.
The Reuleaux Triangle does not have a clear radius, but is still diametrically constant, much like the Meissner tetrahedron.
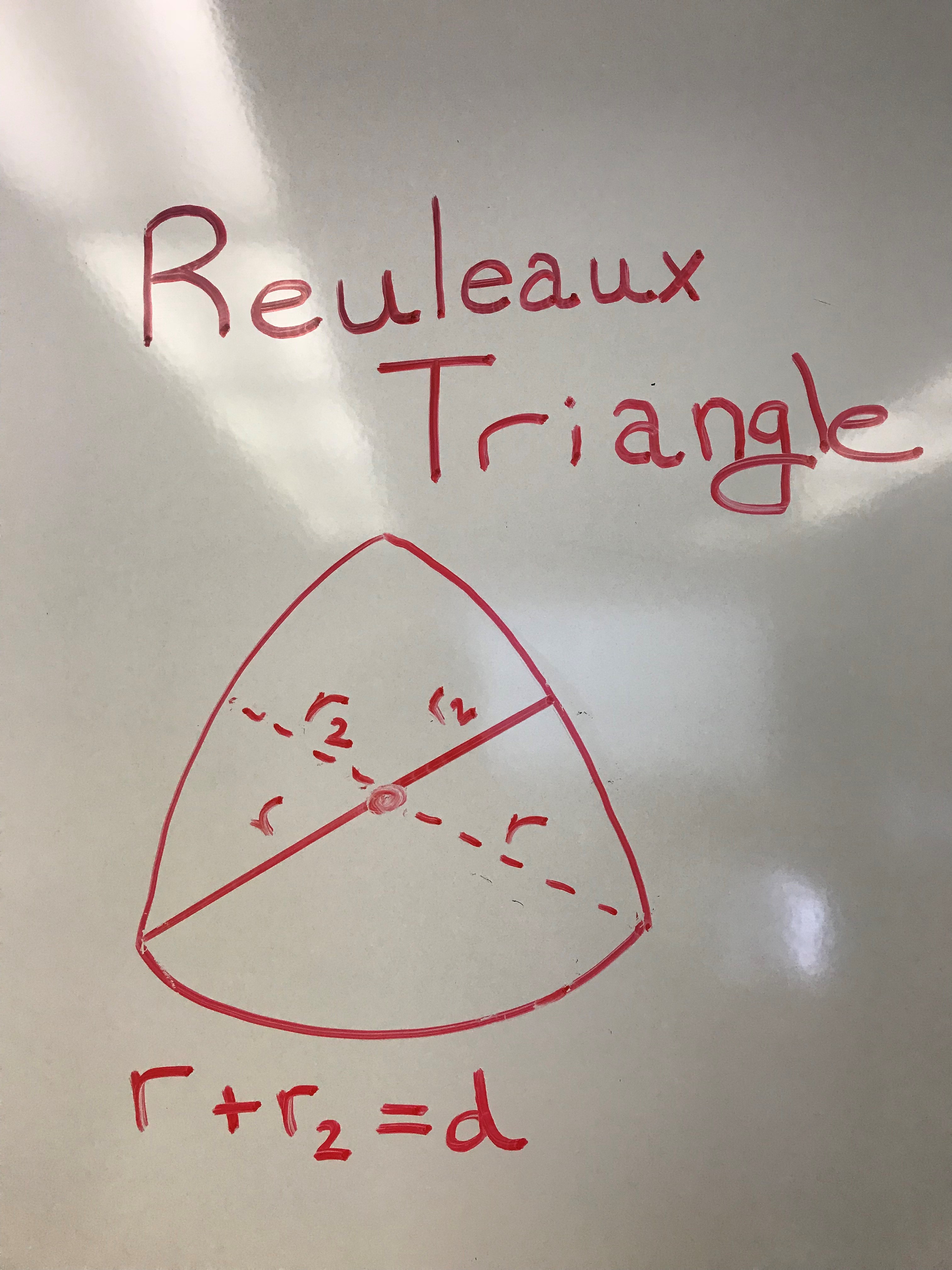
When you rotate the triangle, the center is always moving, so a radius can never be constant. However, due to this, rather than create a perfect, spherical outline, this allows the Reuleaux Triangle to rotate not only within a square, but create a square-border as well. This is shown below where the boundary of the square is displayed as well as the center that will constantly change based upon what part of the object is actually at the bottom of the square.

The square with the borders is very important because it is actually used in some peoples day-to-day life. In the case of Henry Watt’s Square Drill, which uses the tetrahedron to actually drill a square into the wall shown in the video below. A carpenter can now drill a perfect square in less than a minute rather than having to do multiple cuts.
Although we gave many points as to why the Meissner tetrahedron acts and works like a sphere, ultimately it is not capable of being used in all designs and equipment that function with a circle. In the case of the bike or even a car, the tetrahedron wouldn’t work because the axis in a vehicle must be at a constant place rather than continuously moving around to follow the constantly changing center of the Meissner tetrahedron.
Link:

The pictures above are the point that we made it to in creating the Meissner Tetrahedron through the fusion software. After this point in following the video, our diagram wasn’t cooperating as it should have. We aren’t at what point we made the mistakes but this software as well as design in a whole was much harder to create than expected.