Project Idea
I named my fractal the bird Fractal because I think the removed squares resemble little tiny bird. To create this , I removed (0,0), (1,1), (3,1), (1,3), and (3,3). The surface area for level one is 11 because we started out with 16 pieces total, and I removed 5 pieces. The area for level two would be 10.31, and the level three would be 7.95.
Below images are my prints of four levels.
 Level 1
Level 1
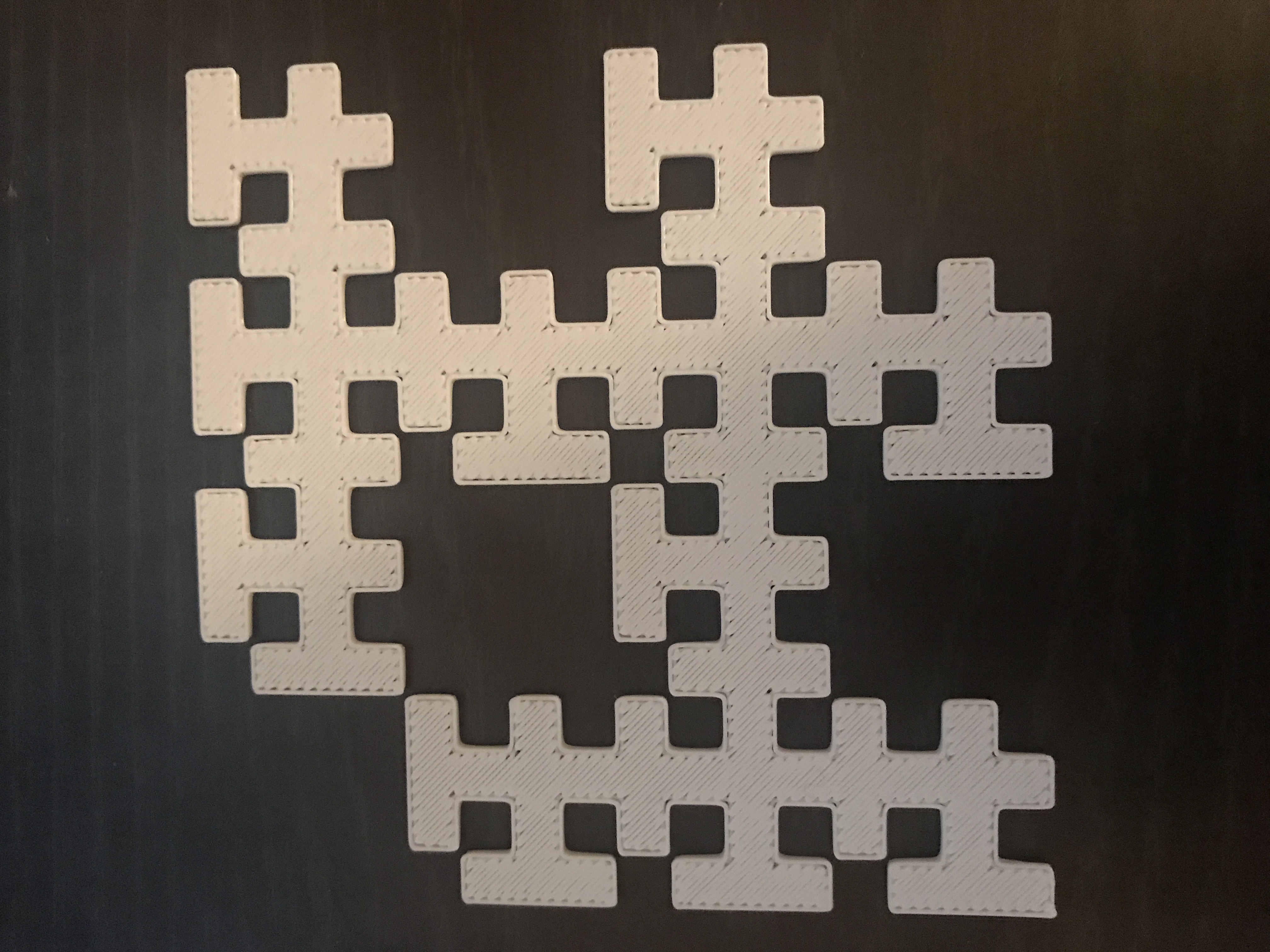 Level 2
Level 2
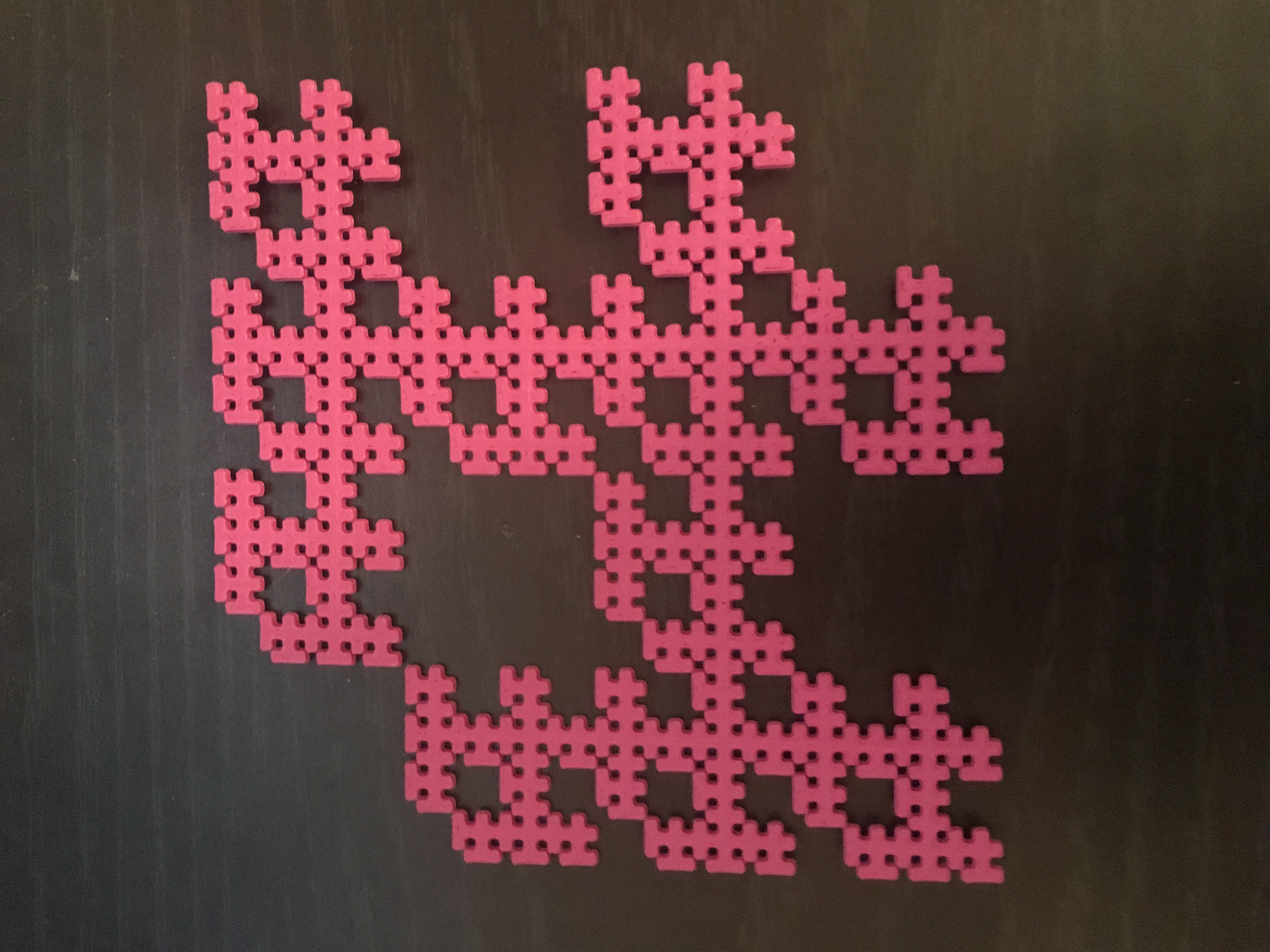 Level 3
Level 3
 Level 4
Level 4
Sum Calculations
Below is the equation used to calculate surface area of level 1, 2, and 3 of the bird fractal.

For each level, I just use total area before moving minus the area that removed. However, for next level, five squares have been moved. So we need to multiply by 11 with area each time.
Like the formula, I write down on the paper.
Level 1: area of removed= 3*(1*1)
Level 2: area of removed=3*11*(1/4*1/4)
Level 3: area of removed=3*11*11*(1/16*1/16)
Dimension
Finally, the sum of an infinite series. to calculate this, I had to find a and r. Then, follow the equation of a + ar + ar^2 + ar^3 + ar^4… if |r| < 1, and then I had to plug in ‘a’ and ‘r’ in the formula of a x 1/(1- r) which ended up equally 16 so that cancelled out the initial area of 16, which equals to zero.
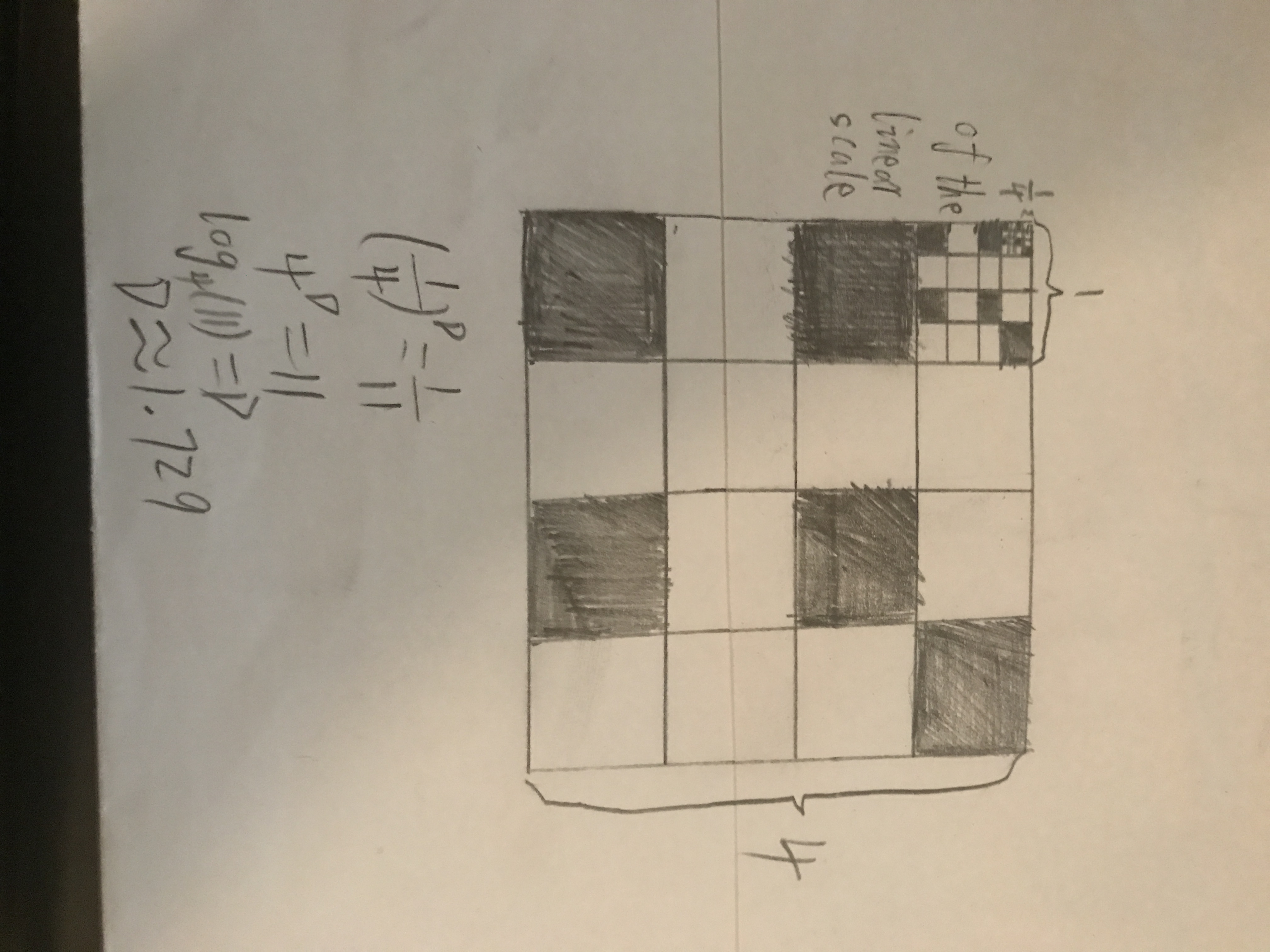
It is scaled down by 1/4 from Level 1 to Level 2, and the same as Level 2 to Level 3. As I marked, the smaller copy of the whole fractal and the larger one is 11 copies of the big one. For my fractal, I cut down three squares in each box. It means the little square is 1/11 of the whole fractal.
Above, I use the formula to calculate dimension, which is (1/4) ^D=1/11.
As I write down on the paper, I use log formula to get Dimension. At last, it came out the dimension is D=1.729.
Thingiverse
Make it yourself by finding the files in https://www.thingiverse.com/thing:2712626