Sunflower Fractal

Nathan Glass (Designer)

Summer Xia (Math)

Michael Conway (Writer)

Introduction-First Design

After studying fractals in class for the past few weeks, our group decided to try to make our own. In making our fractal we decided to go for a sunflower type shape with a hollow center, where the image repeats by halving its size and repeating inside the center of the original image. Upon continual zooming in on the center of this image, this will cause a space filling effect, similar to that of a dragon curve or other similar fractals.

Math

While this is only the 2nd iteration, the repeating halving and repeating of this design would create an apparition  of a never ending tunnel as one zooms in on it. The figure is composed of 18 cog rings with 18 “high stars” attached to them.  The 18 cog rings are 20 degrees each, so 360 degrees in a circle/20 degrees each make for 18 high stars on each iteration. Upon repeating the image, the diameter of the circular figure is cut in half from 110mm to 55mm and the second iteration is placed inside the 55mm hole in the center. To make a third iteration would get cut in half to 25.5mm in diameter and get placed inside the inner circle of the second iteration figure. This would same math of cutting the previous iteration in half and placing it in the center of the prior one would continue into infinity.

3D Printing

The current design will be easier to 3D print than the previous design we had, as the previous one we had a bit of a UFO side profile to it, making minimal contact with the 3D printers pad and we never had success printing that, so we made the bottom end flat to ensure one side made continual contact with the platform and would give our fractal more of a pyramidal side profile, thus making it easier to print.

Volume Calculations

Because of the extremely complex nature of our designed fractal, we are using the Sierpinski Carpet/Menger Sponge. The Menger Sponge is simply the 3 dimensional version of the Sierpinski Carpet.

****Note: All units are mm****

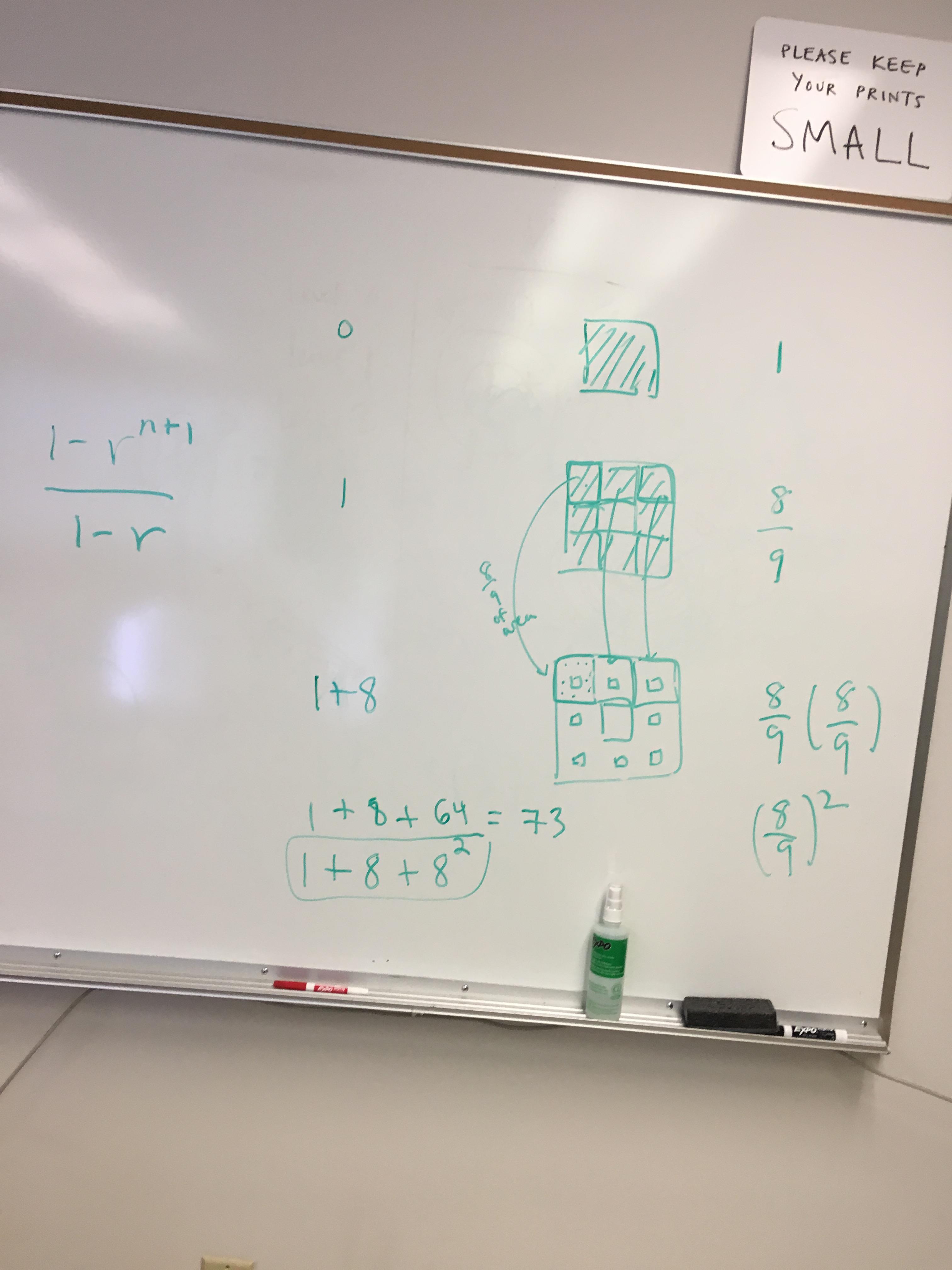
(Photo above) The work in the image above clearly illustrates the calculations that were done to find the area of the surface of our fractal and the number of cut out squares in the fractal. Area is simply 1+1(8/9)^1+1(8/9)^2+1(8/9)^3 and you would keep repeating the pattern, increasing the exponent by one each time until it reached the number of iteration that you wanted. wolframalpha.com is a hyper-powerful online logarithmic calculator that you can use to make solving these long equations easy.

The formula we used to figure these calculations out is +1(1/1-r). Assuming you had infinite time, you could calculate any level (or “r” in the formula) of this fractal into the infinite level.

(Photo Below)  This photo clearly illustrates the problem solving process used to calculate the number of squares in each iteration of the Menger Sponge. Iteration Zero is just simply a solid square, while iteration one has one large square in the center that is 1/9th the size of the original square, meaning 8/9ths are still solid object. The second iteration, each of the 8 “border squares” get one hole in the center of them, like in the 1st iteration. The formula now becomes 1+(8/9)^2. this is repeated as the pattern continues into infinity, as demonstrated below. The number of small squares in the increases, covering a total of 1/9th of the total area at every level, as the solid figure will always occupy the other 8/9ths of the total area at every level.

Fractal Dimension

To find the dimension of our fractal, we used the following calculation:

(1/3)^D = (1/8)

3^D = 8

D=(log3)8=(log8/log3)

=1.8928

What this problem is essentially saying is that the little cube is always 1/8th the volume of the large cube, and the large square divided into 1/3 of itself will result in the first iteration of the cube.

Our final thingverse post for our fractal is found here.