Firework Fractal

Group Members

Haleigh Sink (Designer)
Isabelle Murakami (Writer)
Caitlyn Benjamin (Math Consultant)

First Design Iteration

For our first design, we wanted to go with something that was simple to create but flexible to expand on. As of now, our design is made up of different sized shape of gears. We started off with the center gear being 60×60 and then went down by a third each time, so the next size was 20×20 and then 6.66×6.66. Instead of adding a gear to each spoke, we went every other to keep it cleaner.

3D Printing Results

Our design took over two hours to print but it came out extremely well. The spokes are easily seen, even as they get smaller. We’re pretty happy about it and since this was just our first iteration, we went with a flat design. However, we are hoping to change the height of each gear to make it more 3-dimensional.

 

 

 

Length and Area Calculations

We assumed an area of 1 for our initial level (level 0). Since we scaled down our original shape or “gear” by a third each level, both by its length and width, we would actually use (1/9) in our equation and then we raise it to the power of the exponent of each specific iteration level. Since the number of gears added multiplies by 4 with each iteration we took the number of level 1 iteration gears, 4, and raised it to the power of the exponent of each specific iteration level. We raised the (1/9) and the 4 with their respective exponents (which were determined by iteration level) and added the original area of 1 in order to find each levels accurate number of gears and proper gear scaling, even though they become too small to see as the iterations continue.

Here is the area equation used to find the decimal values up to level 100 of our Firework Fractal.

Level                                            Area                                               Decimal Value

0                                                       1                                                              1

1                                                   1+4(1/9)                                                   1.11

2                                        1+4^2(1/9)^2                                                    1.32

3                                  1+4^2(1/9)^2+4^3(1/9)^3                                  1.41

4                        1+4^2(1/9)^2+4^3(1/9)^3+4^4(1/9)^4                    1.45

5        1+4^2(1/9)^2+4^3(1/9)^3+4^4(1/9)^4+4^5(1/9)^5            1.46

100          1+4^2(1/9)^2+4^3(1/9)^3…+4^100(1/9)^100

n              1+4^2(1/9)^2+4^3(1/9)^3…+4^n(1/9)^n

 

The area of the fractal is finite because its decimal value only goes up slightly every iteration, so it will continue to not exceed a bounded area.

Fractal Dimension

Our fractal proved to be incalculable regarding it’s dimension so we calculated the dimension of another fractal that a group member printed, the Koch Snowflake, displayed here.

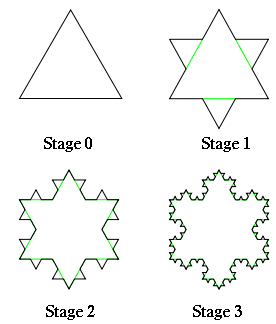
The Koch Snowflake shrinks down by a third each iteration, which you can see explained by the diagram in the picture below where the pattern has become 1/3 the length of the original iteration of the Koch Snowflake. So you would  take 1/3 to the unknown dimension. On the other side of the equation we are finding 1 over the number of copies and since the pattern increases by 4 copies each iteration you would plug in 4 for the number of copies. You can also see how the number of copies increases by 4 in the picture below.

Equation: (scale-down factor)^(dimension)=1/(number of copies)

=(1/3)^D=(1)/(4)

=1.26185

You can see this equation and how the values for the equation came from the Koch Snowflake in the visual below.

Geometric Series

So, we found the area of the Firework Fractal and now have to calculate the geometric series. We use this equation to calculate an infinite geometric series   Following this formula we plug in our fractal’s numbers.

Equation: a + ar + ar^2 + ar^3 +…..

The area of our fractal in it’s original state is 1, so we plug that into the variable a.

1 + 1r + 1r^2 + 1r^3…..

Our fractal size decreases by 1/9 because as stated earlier we take both sides of the gear and shrink them down by 1/3 each iteration (1/3 x 1/3=1/9). So for each level we would multiply that 1/9 times 4, which is the number of gears that are added each iteration. Simplifying that into  1/9 x 4=4/9,  so we plug in (4/9) for the variable r.

1 + 1(4/9) + 1(4/9)^2 + 1(4/9)^3…..

Below is a visualization that helps better understand how the equation is applied to our fractal’s iterations.

Here you can see the geometric series of a number of iterations going up to level 100 and their calculations.

1 + 1( 4/9)^1 + 1(4/9)^2 + 1(4/9)^3… + (4/9)^100

= .44444444444 + .1975308642 + .0877914952 + 6.04989999E-36

If r <1 than the series is infinite and the formula A (1/(1-r)) will be used to find the sum.

1/9<1 so the series is infinite.

Plugging in the area of the fractal for a (1) and the r-value (1/9) the calculation comes to .888888889.

a(1/1-r)=1(1/1-(1/9))=.888888889

Thingiverse

You can download a free copy of our Firework Fractal on Thingiverse

or view it on Tinkercad