Pyramid Spiral Fractal

Group Members

Madeline Biggins (Designer)
Jenna Jordan (Math Consultant)
Jennifer Marks (Writer)

First Design Iteration

For our first fractal we wanted to start with the shape of a pyramid. The first pyramid is 30x30x30. To start we shift a copy of the pyramid up by 2. From there all of the dimensions are decreased by 2 mm and tilted by 22. 5 degrees. We then used Command D to repeat this process. While practicing on Tinkercad we liked the Command D function. We felt that it was a good way to create a mathematically accurate fractal since it just repeats it’s first action.

    

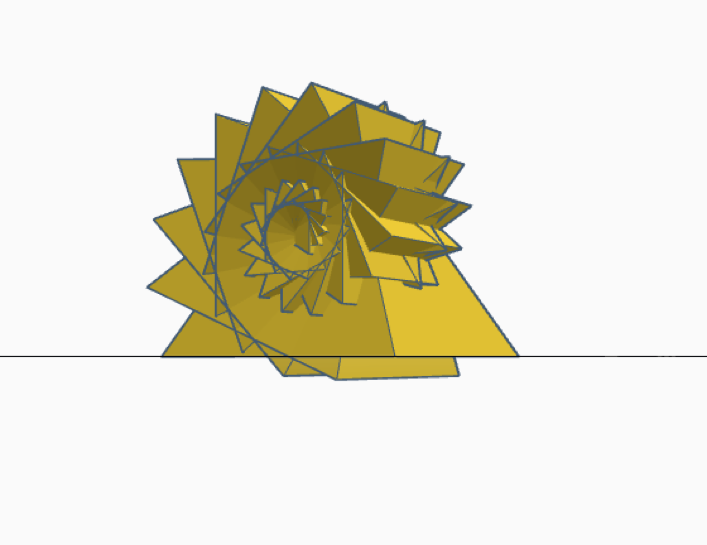
We all really like the design. So far we believe that this is a viable fractal but we will have to check our math with Dr. Taalman to be sure. It has the basic concept of a fractal in that the pyramid shape is tilted repeatedly. We believe that this process could be done infinitely.

Updated Design and First Print

During class were made some adjustments to our initial design. The first pyramid is still 30x30x30 but the second pyramid is shifted 5 millimeters up instead of 2. Shifting the second pyramid farther upward eliminated the issue we had of the tops of the pyramids in the first few iterations poking out if the bottom of the fractal. Each iteration is still tilted by 22.5 degrees. Each iteration is 93% of the size of the iteration before. One of the formulas we will need for this fractal will be V= lwh/3. For our first print of the Spiral Pyramid we printed a level 20 iteration. We generated supports for this print and once they were removed the print look exactly as we designed it.

 

   

Perimeter Calculations

Since our fractal had overlapping 3 dimensional properties we decided the calculations would be too hard for us to complete. Instead we decided to use Maddy’s first fractal, the Koch Snowflake. We care calculating the perimeter of the 1st, 2nd, 100th, and ∞ iterations. The Koch snowflake has an infinite perimeter but a finite area. We got the 4/3 value for our calculations since each side of the triangle is being divided into thirds.

 

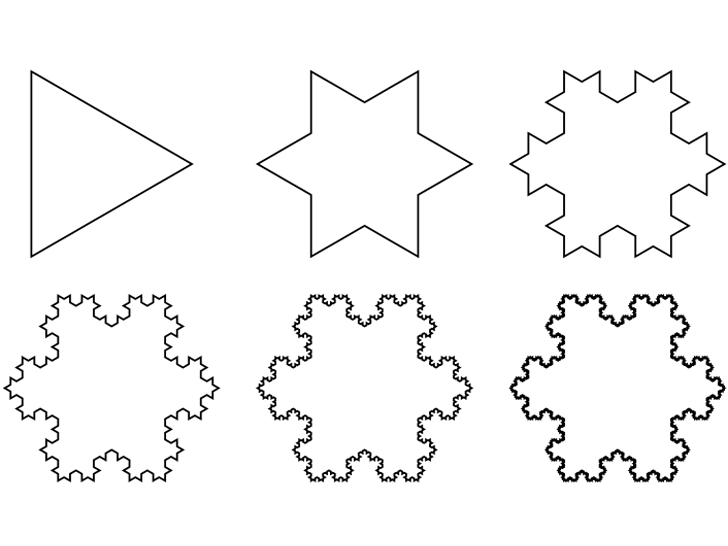
Level 0
P= (4/3)^0 × 3
P= 1×3
P=3

Level 1
P=(4/3)^1 × 3
P= 4/3 × 3/1= 12/3
P= 4

Level 2
P= (4/3)^2 × 3
P= 16/9 × 3/1= 48/9
P= 5 1/3 or 16/3

Level 100
P= (4/3)^100 × 3
P= 9.35 × 10^12

Level n
P= (4/3)^n × 3

Level ∞
P= (4/3)^∞ × 3

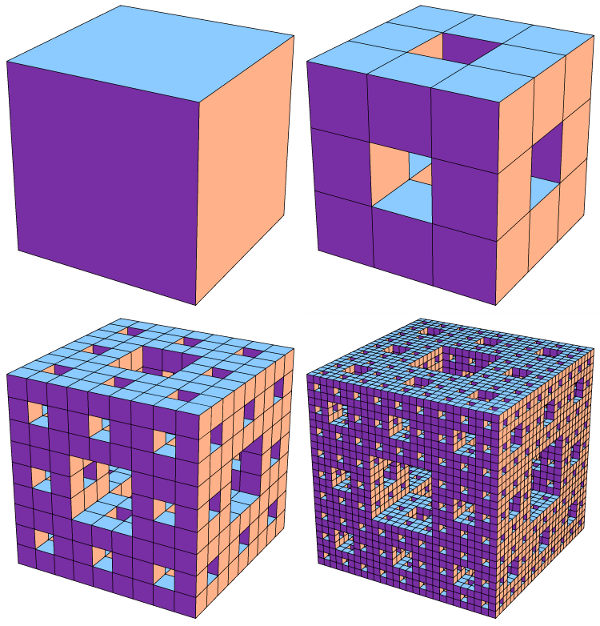
Fractal Dimension

Once again our Pyramid Spiral Fractal was too complex for us to easily calculate it’s dimensions due to it’s overlapping properties. For this calculation we decided to use Jennifer’s first fractal, the Menger Sponge. We calculated the dimension of a level 2 Menger Sponge. In each iteration each cube is 1/3 the size of the first. In the second iteration there are 20 cubes. In our equation D stands for dimension. S stands for the scale. N stands for the number of cubes in the iteration. We looked at the cube example on the board and knew the process for finding the dimension of the Menger Sponge would be somewhat similar. We knew we needed a log since there are empty spaces within the fractal.

Dimension is S^D= 1/N

(1/3)^D=1/20
Log3 20 ≈  2.726833

 

 

Thingiverse

Click here to see our Spiral Pyramid Fractal!

Here’s a link to our fractal on Tinkercad!